Find the equivalent resistance between the point a and b of the circuit shown in figure
To find the equivalent resistance between points A and B in the given circuit, we can follow these steps:
Step 1: Identify the Configuration
First, we need to analyze the circuit configuration. The circuit consists of multiple resistors, and we need to determine if it forms a Wheatstone bridge or any other configuration.
Step 2: Check for Wheatstone Bridge
In this case, we need to check if the circuit forms a balanced or unbalanced Wheatstone bridge. A balanced Wheatstone bridge has the property that the ratio of the resistances in one branch is equal to the ratio in the other branch. If it is unbalanced, we will have to use the current division method.
Step 3: Assign Currents
Assume a current i enters the circuit at point A. This current will split into two branches. Let i1 be the current flowing through one branch and i−i1 be the current flowing through the other branch.
Step 4: Apply Kirchhoff's Laws
Using Kirchhoff's Voltage Law (KVL), we can write the equations for the potential differences across the resistors.
1. For the branch with resistance 10Ω:
VA−VC=i1×10
2. For the branch with resistance 5Ω:
VC−VB=(i−i1)×5
Step 5: Combine the Equations
We can express VA−VB as:
VA−VB=(VA−VC)+(VC−VB)=10i1+5(i−i1)
This simplifies to:
VA−VB=10i1+5i−5i1=5i+5i1
Step 6: Find the Equivalent Resistance
To find the equivalent resistance Req, we use the formula:
Req=VA−VBi
Substituting the expression we derived:
Req=5i+5i1i
Step 7: Eliminate i1
To eliminate i1, we can express it in terms of i using the current division rule or by manipulating our equations. After substituting and simplifying, we find:
Req=7Ω
Conclusion
The equivalent resistance between points A and B is 7Ω.
---
First, we need to analyze the circuit configuration. The circuit consists of multiple resistors, and we need to determine if it forms a Wheatstone bridge or any other configuration.
In this case, we need to check if the circuit forms a balanced or unbalanced Wheatstone bridge. A balanced Wheatstone bridge has the property that the ratio of the resistances in one branch is equal to the ratio in the other branch. If it is unbalanced, we will have to use the current division method.
Assume a current i enters the circuit at point A. This current will split into two branches. Let i1 be the current flowing through one branch and i−i1 be the current flowing through the other branch.
Using Kirchhoff's Voltage Law (KVL), we can write the equations for the potential differences across the resistors.
VA−VC=i1×10
2. For the branch with resistance 5Ω:
VC−VB=(i−i1)×5
We can express VA−VB as:
VA−VB=(VA−VC)+(VC−VB)=10i1+5(i−i1)
This simplifies to:
VA−VB=10i1+5i−5i1=5i+5i1
To find the equivalent resistance Req, we use the formula:
Req=VA−VBi
Substituting the expression we derived:
Req=5i+5i1i
To eliminate i1, we can express it in terms of i using the current division rule or by manipulating our equations. After substituting and simplifying, we find:
Req=7Ω
The equivalent resistance between points A and B is 7Ω.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - worked out Example
1 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Short Answer
17 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Exercises
84 Videos
- DISPERSION AND SPECTRABOOK - HC VERMACHAPTER - DISPERSION AND SPECTRAEXERCISE - Exercises
11 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
Similar Questions
Knowledge Check
Find the equivalent resistance between the point a and b of the network shown in figure.
 A3B2C1D5
A3B2C1D5The equivalent resistance between the points A and B in A the circuit shown in Fig. is
 A3.12ΩB1.56ΩC6.24ΩD12.48Ω
A3.12ΩB1.56ΩC6.24ΩD12.48ΩThe equivalent resistance between point x and y, of the circuit as shown in the figure is
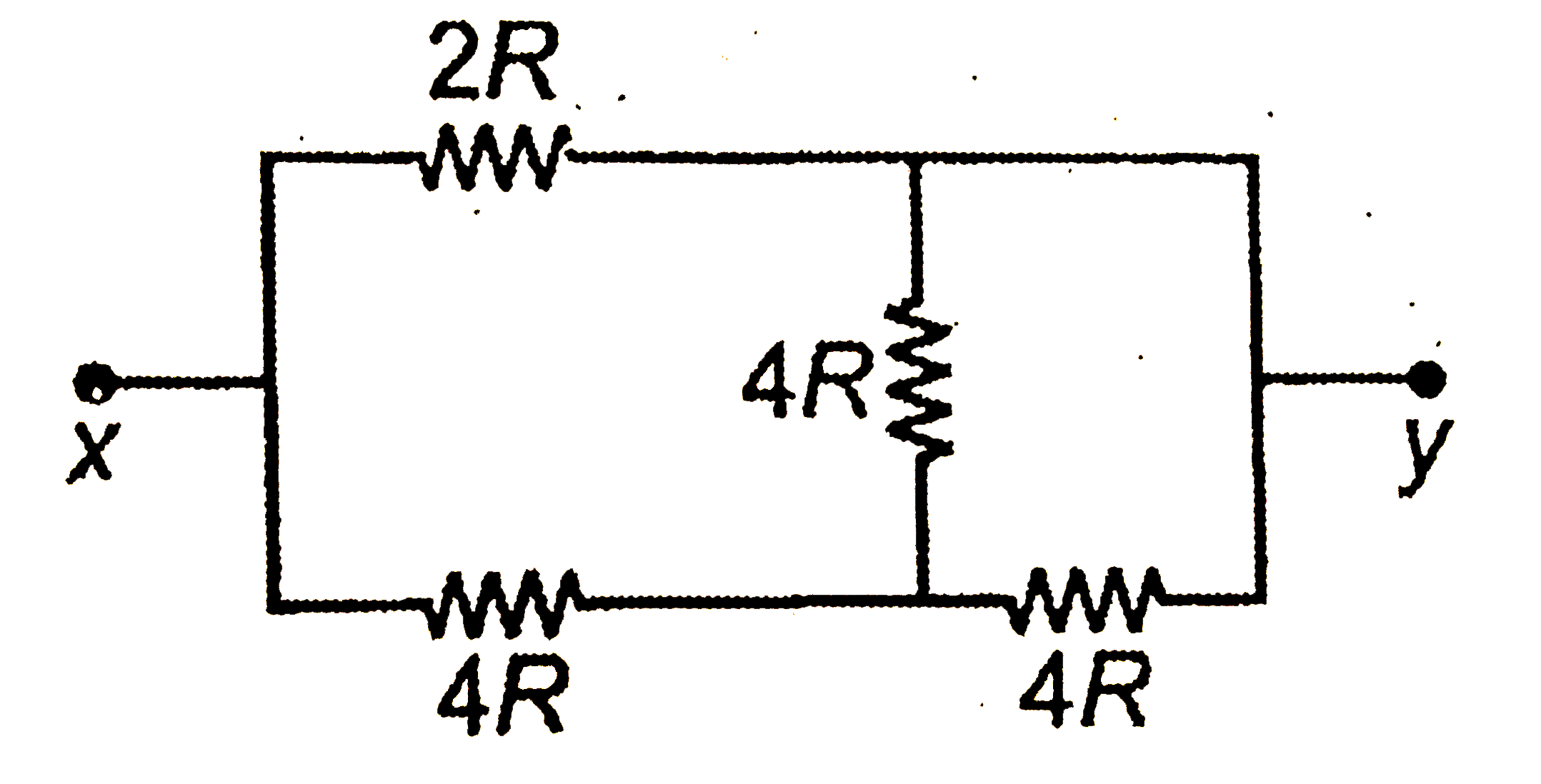 ARB3R2C3R4D8R5
ARB3R2C3R4D8R5
Calculate the equivalent resistances between the points AandB of the circuits shown in (fig. 2.33)(b).
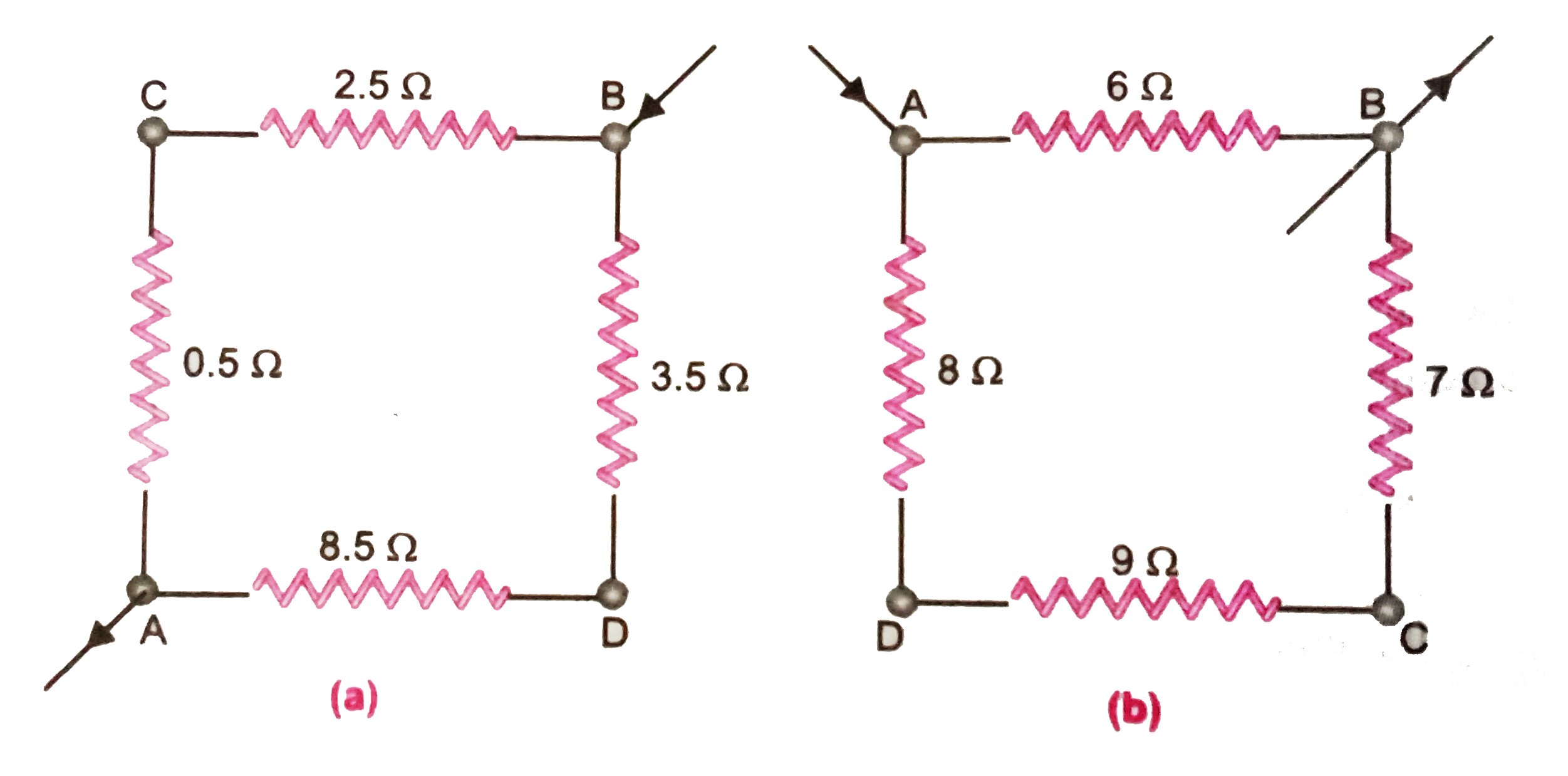 .
.
View SolutionFind equivalent resistance between points A and B in the circuit shown.
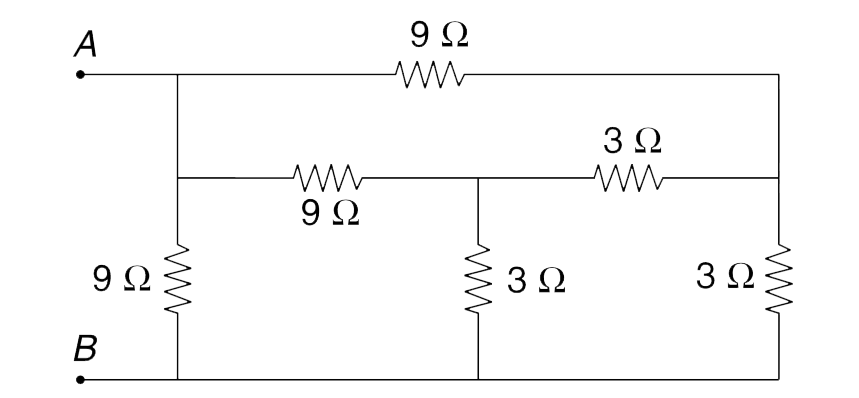
View SolutionFind the equivalent resistance between point a and b in the network shown in figure.
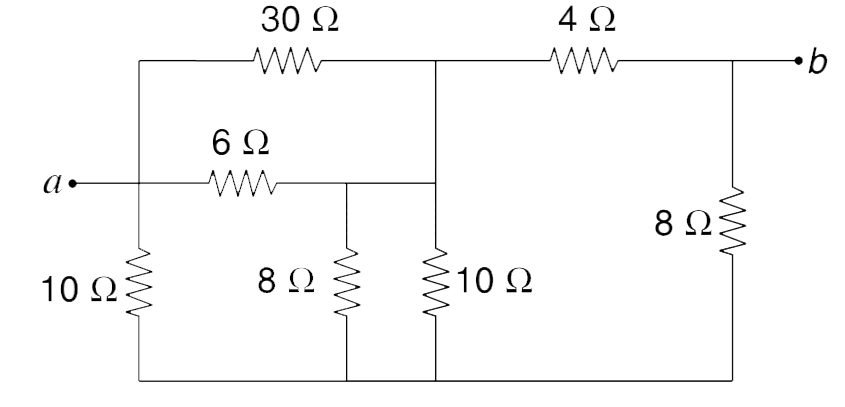
View SolutionCalculate the equivalent resistance between the points A and B of the network shown in figure

View SolutionCalculate the equivalent resistance between the points A and B of the network shown in figure
View Solution

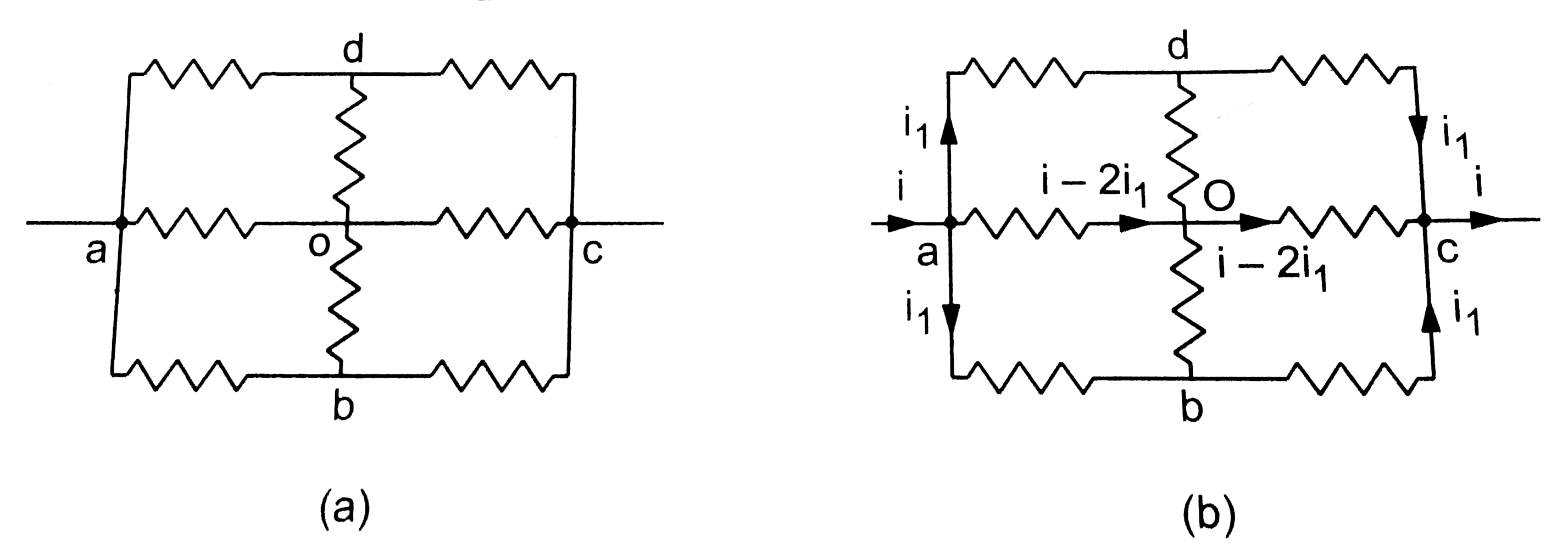
_PHY_E05_095_Q01.png)