Two particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
acceleration of both the particles are equal.
acceleration of the particle of mass m1 is proportional to m1
acceleration the particle of mass m1 is proportional to m2.
accelaration of the particle of mass m1 is inversely proportional to m1.
The correct Answer is:C
Given situation is shown in the figure. Gravitational force,
F=Gm1m2r2
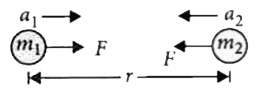
Acceleration of particle of mass m1a1Fm1=Gm2r2
∴a1∝m2.
Topper's Solved these Questions
- GRAVITATIONBOOK - MTG-WBJEECHAPTER - GRAVITATIONEXERCISE - WB JEE WORKOUT CATEGORY 3 : One or More than One Option Correct Type
10 Videos
- ELECTROSTATICSBOOK - MTG-WBJEECHAPTER - ELECTROSTATICSEXERCISE - (WB JEE Previous Years Questions ) CATEGORY 3 : One or More than One Opion correct Type
4 Videos
- HEAT AND THERMAL PHYSICSBOOK - MTG-WBJEECHAPTER - HEAT AND THERMAL PHYSICSEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
15 Videos
Similar Questions
Two particles of mass m1 and m2 are approaching towards each other under their mutual gravitational field. If the speed of the particle is v, the speed of the center of mass of the system is equal to :
View SolutionTwo particles A and B of mass 1 kg and 4 kg respectively approach each other due to their mutual gravitational force only. Then the ratio of acceleration of A to B at any instant is
View Solution
Knowledge Check
Two particles of mass m1 and m2 are approaching towards each other under their mutual gravitational field. If the speed of the particle is v, the speed of the center of mass of the system is equal to :
Am1m2vBZeroC(m1−m2)vm1+m2Dm2m1vTwo particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
AV=12R√1GmBV=√GM2RCV=12√GmRDV=√4GmR2 bodies of different masses of 2 kg and 4 kg are moving with velocities 20m/s and 10 m//s towards each other due to mutual gravitational attraction. What is the velocity of their centre of mass?
A5ms−1B6ms−1C8ms−1DZero
Two particles A and B of mass 1 kg and 4 kg respectively approach each other due to their mutual gravitational force only. Then the ratio of acceleration of A to B at any instant is
View SolutionTwo particles of equal mass m0 are moving round a circle of radius r due to their mutual gravitational interaction. Find the time period of each particle.
View SolutionTwo particles of equal mass m0 are moving round a circle of radius r due to their mutual gravitational interaction. Find the time period of each particle.
View SolutionTwo bodies of masses 2 kg and 4 kg are moving with velocities 2 m s−1 and 10 m s−1 towards each other due to mutual gravitational attraction. What is the velocity of their centre of mass?
View SolutionFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
View Solution
