A uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:

2π√mk
2π√2m3k
π√3m2k
π√2m3k
Let centre of disc is displaced by x from its equilibrium position (spring was in its natural length). Now calculate the torque about lowest point of disc.
k.32R.3x2=32mR2aR
3kx2m=a
So, T=2π√2m3k
Topper's Solved these Questions
Similar Questions
A block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is

View SolutionA spring of force constant k is connected with centre of a disc of mass m and radius R System is placed on honzontal surface and other end of spring is fixed with a vertical wall as shown in a figure. If there is sufficient friction for pure rolling then time period of oscillation of the disc will be
View Solution
Knowledge Check
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m

A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
View SolutionA solid cylinder is attached to a horizonatal massless spring as shwn in figure.If the cyclinder rolls without slipping, the time period of oscillation of the cyclinder is

View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
 .
.
View SolutionA small block of mass 2 kg is placed on a bigger block of mass 4 kg which is attached to horizontal spring of spring constant K=500N/m as shown in figure, coefficient of friction between block is 0.2 .Maximum amplitude of system so that there is no relative slipping between blocks.
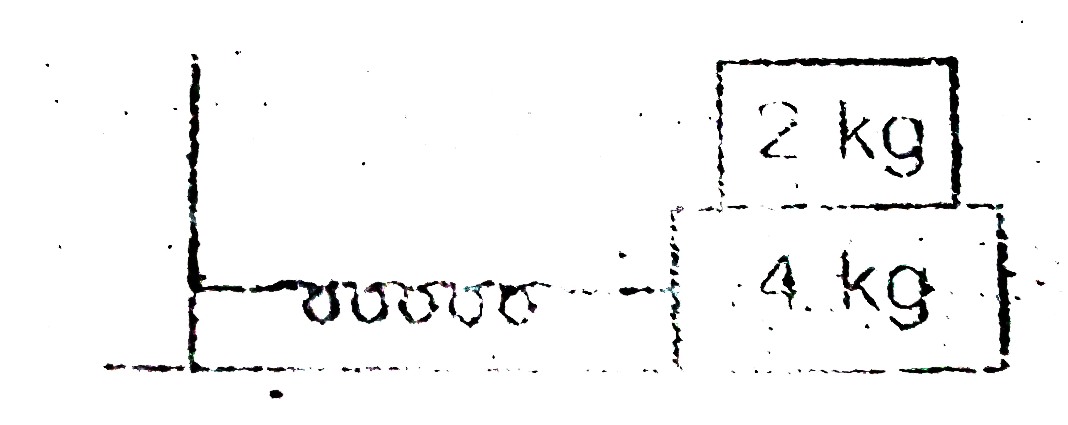
View SolutionA solid sphere rolls without slipping and presses a spring of spring constant k as shown in figure. Then, the compression in the spring will be
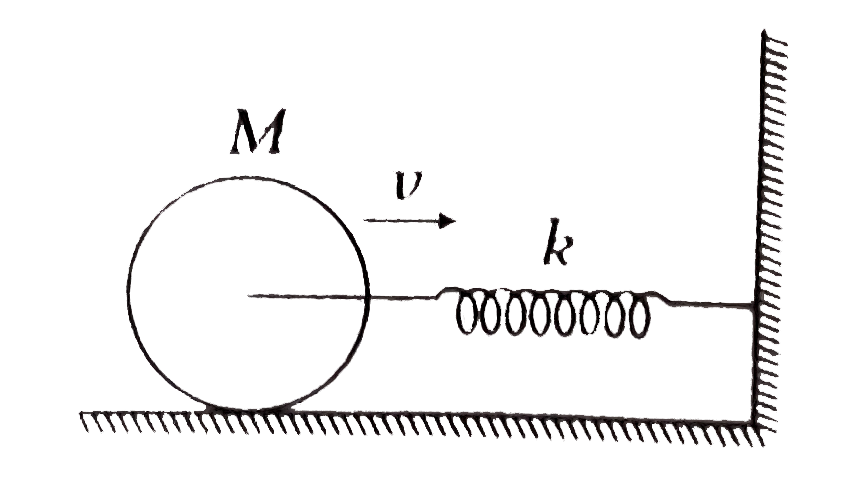
View SolutionA uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
