Four resistors, 100 $Ω, 200 Ω, 300 Ω and 400 Ω$ are connected to form four sides of a square. The resistors can be connected in any order. What is the maximum possible equivalent resistance across the diagonal of the square?

A

$210 Ω$

B

$240 Ω$

C

$300 Ω$

D

$250 Ω$

Text Solution

Verified by Experts

The correct Answer is:D

In the figure, resistors 2R and 3R are in series.
$∴$ Equivalent resistance, $R_{1} = 2 R + 3 R = 5 R$
Also, R and 4R are in series their equivalent resistance will be,
$R_{2} = R + 4 R = 5 R$

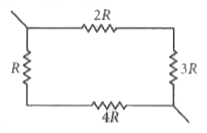
Now $R_{1} and R_{2}$ are in parallel hence maximum equivalent resistance
$R_{e q} = \frac{R_{1} + R_{2}}{R_{1} + R_{2}} = \frac{5}{2} \times 100 = 250 Ω$

|

Updated on:21/07/2023

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Three resistors of $1 Ω, 2 Ω and 3 Ω$ are connected in parallel. The combined resistance of 3 resistors should be
Agreater than $3 Ω$
Blesser than $1 Ω$
Cequal to $2 Ω$
Dbetween $1 Ω and 3 Ω$
Question 2 - Select One
Four resistances $10 Ω, 5 Ω, 7 Ω$ and $3 Ω$ are connected so that they form the sides of a rectangle $A B, B C, C D$ and $D A$ respectively. Another resistance of $10 Ω$ is connected across the diagonal $A C$ . The equivalent resistance between $A$ and $B$ is
A $2 Ω$
B $5 Ω$
C $7 Ω$
D $10 Ω$
Question 3 - Select One
In a circuit four resistors of $1 Ω, 2 Ω, 6 Ω and 12 Ω$ respectively are connected in series combination. The maximum resistance that can be obtained is
A $21 Ω$
B $18 Ω$
C $6 Ω$
D $4 Ω$

MTG-WBJEE-CURRENT ELECTRICITY -WB JEE PREVIOUS YEARS QUESTIONS

Home
Ask Doubt
Profile