कोई चुम्बकीय क्षेत्र B किसी प्रदेश r≤a तक सीमित है तथा इसकी दिशा कागज के लंबतव बाहर की और (z- अक्ष) है r=0 इस वृत्तीय प्रदेश का केंद्र है। m द्रव्यमान तथा त्रिज्या b,(b>a) का कोई आवेशित छल्ला (आवेश Q) जिसका केंद्र मूल बिंदु पर है x-y तल में है। यह छल्ला घूर्णन करने के लिए स्वतंत्र है तथा विराम अवस्था में है। चुम्बकीय क्षेत्र का परिणाम Δt समय में शून्य कर दिया जाता है। चुम्बकीय क्षेत्र समाप्त होने पर छल्ले का कोणीय वेग ω ज्ञात कीजिए।
Step by step video & image solution for कोई चुम्बकीय क्षेत्र B किसी प्रदेश rlea तक सीमित है तथा इसकी दिशा कागज के लंबतव बाहर की और (z- अक्ष) है r=0 इस वृत्तीय प्रदेश का केंद्र है। m द्रव्यमान तथा त्रिज्या b,(bgta) का कोई आवेशित छल्ला (आवेश Q) जिसका केंद्र मूल बिंदु पर है x-y तल में है। यह छल्ला घूर्णन करने के लिए स्वतंत्र है तथा विराम अवस्था में है। चुम्बकीय क्षेत्र का परिणाम Deltat समय में शून्य कर दिया जाता है। चुम्बकीय क्षेत्र समाप्त होने पर छल्ले का कोणीय वेग omega ज्ञात कीजिए। by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR HINDICHAPTER - विद्युतचुम्बकीय प्रेरणEXERCISE - लघुउत्तरीय (SA)5videos
विद्युतचुम्बकीय प्रेरण
- BOOK - NCERT EXEMPLAR HINDICHAPTER - विद्युत धाराEXERCISE - लघुउत्तरीय (LA)4videos
विद्युत धारा
- BOOK - NCERT EXEMPLAR HINDICHAPTER - वैद्युत आवेश तथा क्षेत्र EXERCISE - दीर्घउत्तरीय (LA)6videos
वैद्युत आवेश तथा क्षेत्र
Similar Questions
किसी निश्चित स्थान पर विद्यमान चुम्बकीय क्षेत्र को B=B0cos(ωt)ˆk द्वारा व्यक्त किया गया है तथा इस चुम्बकीय क्षेत्र में x−y तल में प्रतिरोध R तथा त्रिज्या a की कोई कुण्डली रखी है जिसका केंद्र मूल बिंदु पर है। बिंदु (a,0,0) पर t=π2ω,t=πω तथा t=3π2ω समयों पर धारा का परिमाण एवं दिशा ज्ञात कीजिए।
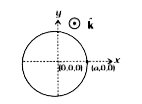 10:31View Solution
10:31View Solutionदो सेल जिनकी वोल्टता 10Ω तथा 2V एवं आन्तरिक प्रतिरोध क्रमश: 10Ω तथा 5Ω हैं, पार्श्वक्रम में इस प्रकार संयोजित हैं कि 10v बैटरी का धनात्मक टर्मिनल 2V बैटरी के ऋणात्मक टर्मिनल से संयोजित है (चित्र 3.8)। संयोजन की प्रभावी वोल्टता तथा प्रभावी प्रतिरोध ज्ञात कीजिए।
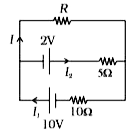 03:29View Solution
03:29View Solutionसन 1959 में लाइटलेटन एवं बॉण्डी ने सुझाया कि यदि द्रव्य पर कोई नेट आवेश हो तो विश्व (यूनिवर्स), के प्रसरण की व्याख्या की जा सकती है। जिनका संख्या घनत्व N है और जिसे और जिसे नियत रखा जाता है, मान लीजिए प्रोटॉन पर आवेश ep=−(1+y)e है, यहाँ e इलेक्ट्रॉनिक आवेश है।
(a) y का वह क्रांतिक मान ज्ञात कीजिए, जिस पर प्रसरण आरम्भ हो सके।
(b) यह दर्शाइए कि प्रसरण का वेग केन्द्र से दूरी के वर्ग के अनुक्रमानुपाती है।02:52View Solutionकोई इलेक्ट्रॉन E=2.0×104 न्यूटन/कुलॉम परिणाम के एकसमान विद्युत क्षेत्र 1.5 से. मी. दुरी तक गिरता है। [चित्र (a )] क्षेत्र का परिणाम समान रखते हुए इनकी दिशा उत्क्रमित कर दी जाती है तथा अब कोई प्रोटॉन इस क्षेत्र में उतनी ही दुरी तक गिरता है [चित्र (b )] दोनों प्रकरणों में गिरने में लगे समय की गणना कीजिए । इस परिस्थिति का 'गुरुत्व के अधीन मुक्त पतन ' से तुलना कीजिए ।
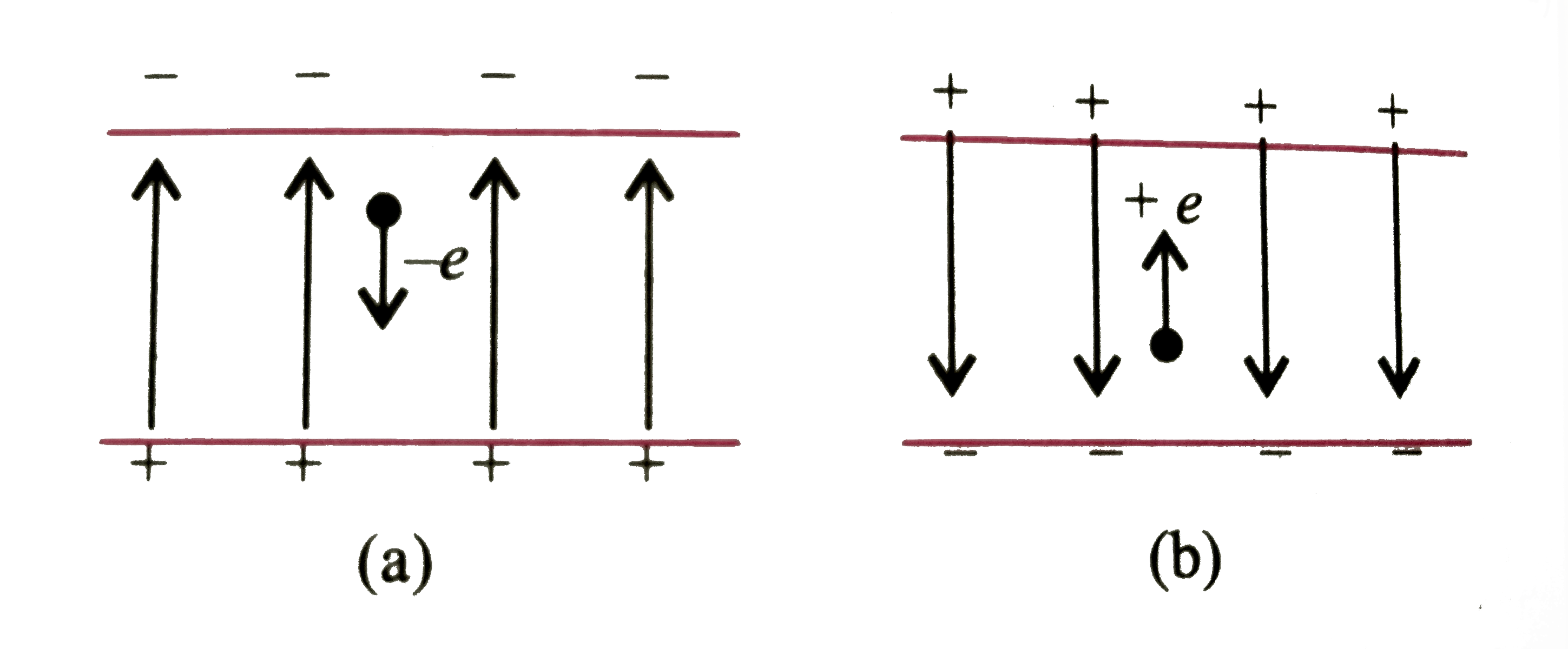 02:54View Solution
02:54View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
04:39View Solutionदी गई आकृति में O वृत्त का केंद्र तथा SCT बिंदु C पर स्पर्श रेखा है। यदि ∠ACS=57∘ हो ,तो ∠OAC की माप है -
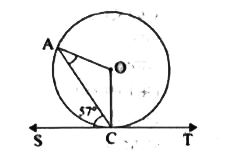 03:33View Solution
03:33View Solutionयदि बिंदु A जिसका स्थिति सदिश ¯a+2¯b है तथा सदिश ¯a,AB को 2:3 के अनुपात में विभाजित करता है तो B का स्थिति सदिश है:
03:53View Solution△ABC के अन्तरगर्त वृत्त का केंद्र O है तथा भुजा AB,BC,CA क्रमशः वृत्त को बिंदु P, Q, R पर स्पर्श करती है। यदि ∠POQ=110∘,∠QOR=120∘ है ,तो ∠CAB का मान है -
03:14View Solutionकोई रेखा x-अक्ष और y-से साथ क्रमशः 60∘ तथा 45∘ के कोण बनाती है। इनके द्वारा घनत्व दिशा में z-अक्ष के साथ कितना कोण बनेगा ?
02:29View Solutionनिम्न कथन सत्य है अथवा असत्य-
वे बिंदु जो सुसंगत क्षेत्र में तथा इसकी सीमा रेखा पर होते हैं, व्यवरोधों (constraints) का सुसंगत हल (feasible solution ) कहलाते हैं।
सुसंगत क्षेत्र के बाहर कोई बिंदु असुसंगत हल (infeasible solution) कहलाता है।07:49View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
02:47View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
02:42View Solutionमाना P(4,−4) तथा Q(9,6) परवलय पर स्थित दो बिन्दु है । O इस परवलय का शीर्ष बिन्दु है तथा X इस परवलय की चाप POQ का कोई ऐसा बिन्दु है, जिसके लिए का ΔPXQ क्षेत्रफल है, तो यह अधिकतम क्षेत्रफल (वर्ग इकाइयो में) है
02:42View Solutionउस दीर्घवृत्त का समीकरण जिसका केंद्र मूलबिन्दु है तथा जो बिन्दुओं (-3, 1) तथा (2, -2) से गुजरता है
01:11View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
01:19:21View Solutionएक वस्तु जिसका द्रव्यमान m है विराम से h ऊँचाई से गुरुत्वीय त्वरण g के अन्तर्गत गिरती है तथा यह रेत में गहराई d तक धंसती है। रेत में फँसने के दौरान औसत मन्दन होगा
45:46View Solution

