A conducting wire carrying current is arranged as shown. The magnetic field at .O.

μ0i12[1R1−1R2]
μ0i12[1R1+1R2]
μ0i6[1R1−1R2]
μ0i6[1R1+1R2]
The correct Answer is:A
B=μ0I4πRθ
B∝1R
B1=μ0I4πR1(π3)μ0I12R1,B2=μ0I4πR2(π3)μ0I12R2
B=B1−B2=μ0I12[1R1−1R2]
Topper's Solved these Questions
Similar Questions
Knowledge Check

A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius RAμ0l2R(1+3ππ)Bμ0l4R(1+3ππ)Cμ0l8R(1+3ππ)Dμ0l8R(2+3ππ)Two perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
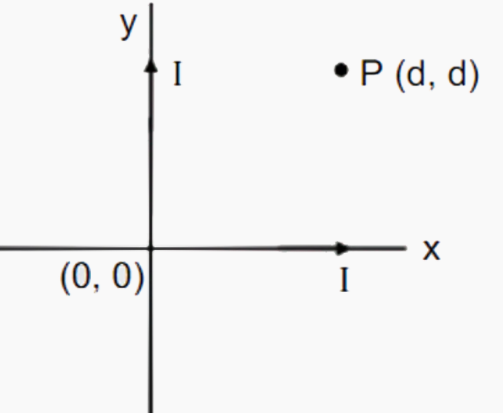 Aμ01πdBμ012πdCμ012πdDZero
Aμ01πdBμ012πdCμ012πdDZeroThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,
 AzeroBμ0I4(1R1−1R2)Cμ0I4(1R2+1R1)Dμ0I2(1R1−1R2)
AzeroBμ0I4(1R1−1R2)Cμ0I4(1R2+1R1)Dμ0I2(1R1−1R2)

A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
View Solution(a) Find the magnetic field at the point O if the wire carrying a current i has the shape shown. The radius of the current part of the wire is R, the linear parts of the wire are very long.
(i)
(ii)
(iii)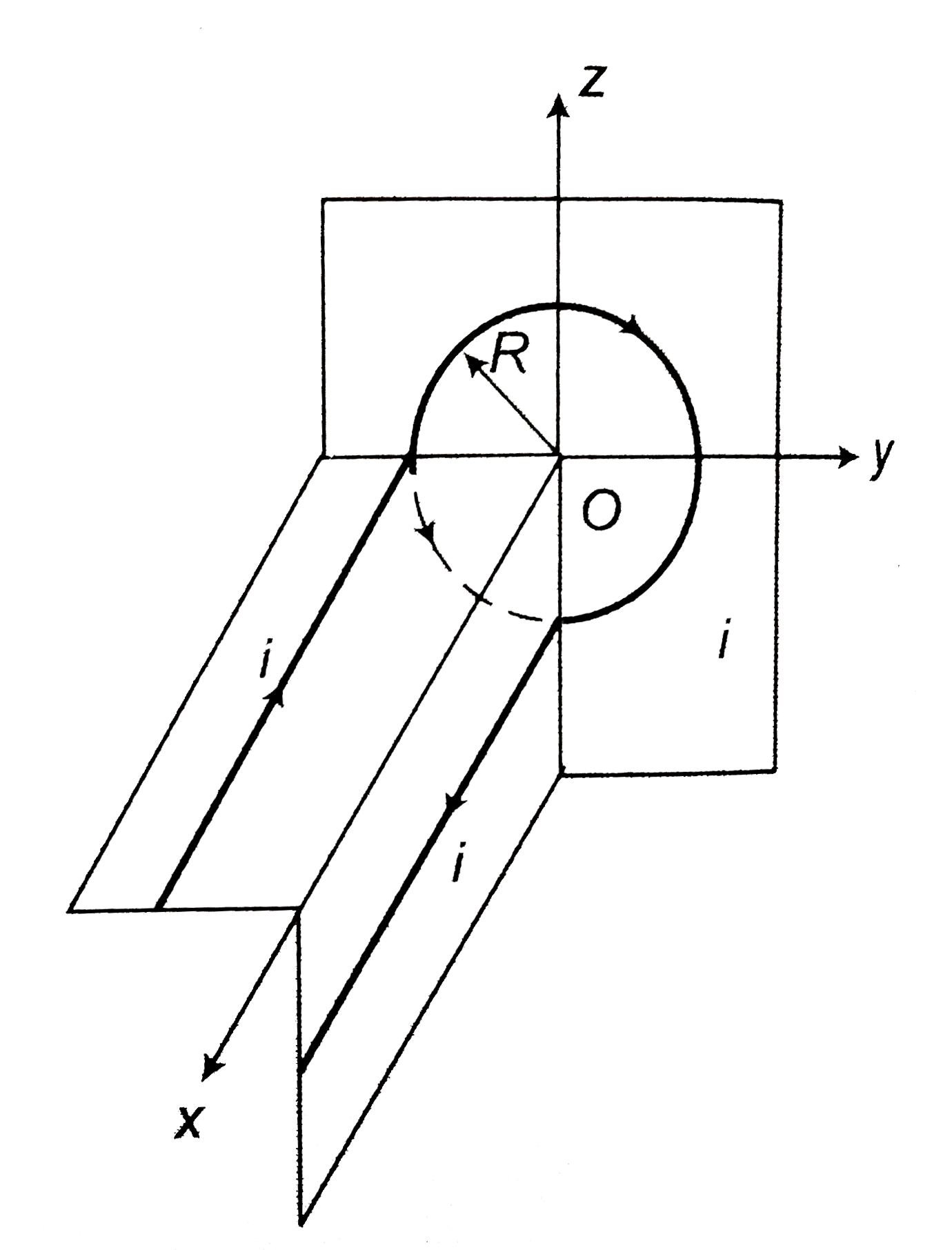
(b) A long straight wire along the z-axis carriers a current i in negative z-direction. Find magnetic field in vector from at a point having co-ordinates (x,y) on z=0 plane.
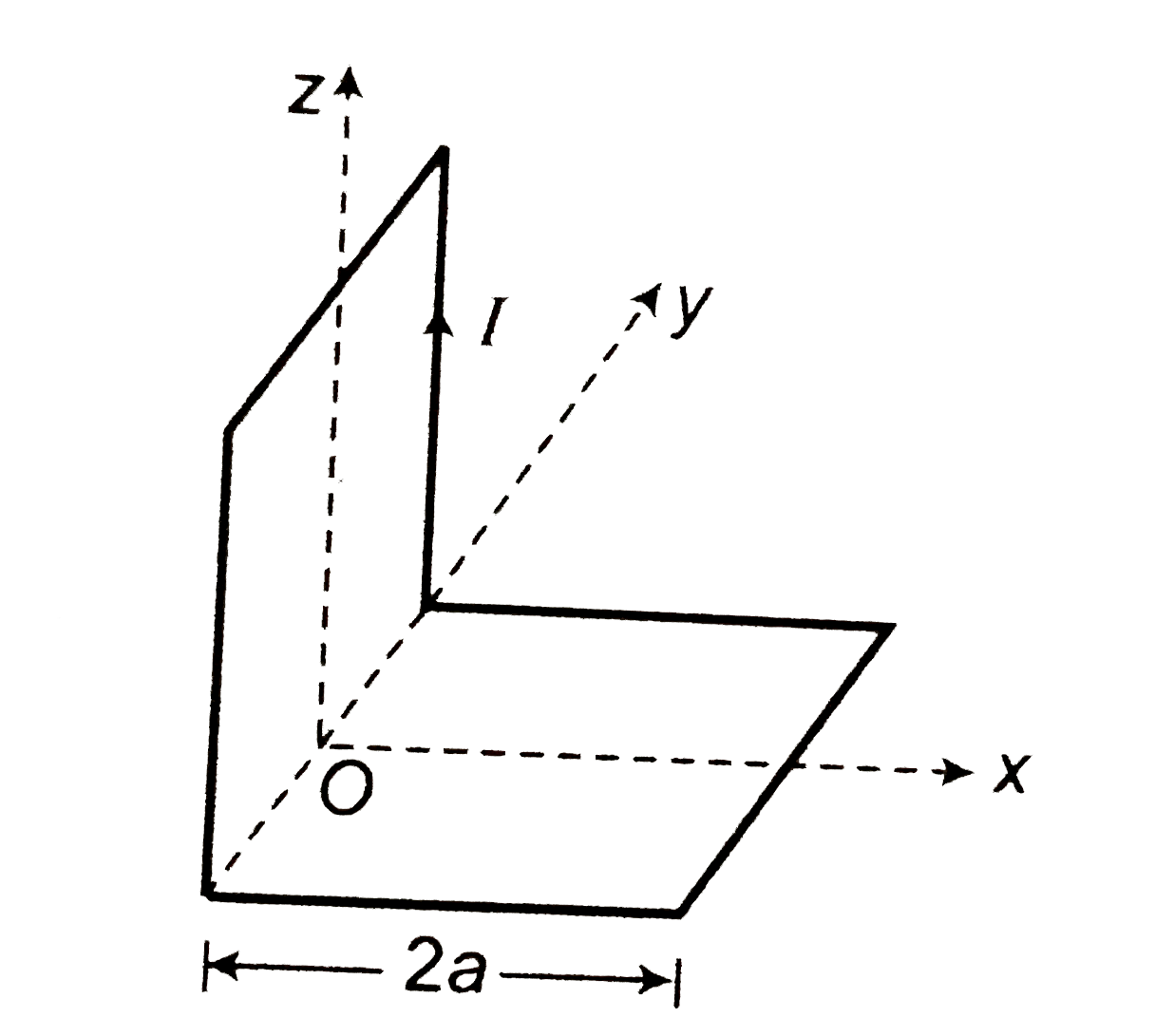
(c) A non-coplaner loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop of length 2a. find unit vector along magnetic field magnetic filed at the point P(a,0,a).
View SolutionTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
_2019_CBT2_E01_008_Q01.png)
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

View Solution

