A stone of mass (m) is attached to one end of a small wire of length (l) and cross-sectional area (A) suspended vertically. The stone is now rotated in horizontal plane such that the wire makes an angle .θ. with vertical. Find the increase in length of wire if its Young.s modulus is Y. Solution in Telugu
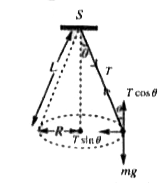
From fig. Tcosθ=mg⇒T=mgcosθ
Tsinθ=mRω2
e=FlAY=TlAY
e=mglAYcosθ
If .θ. was not given but R, w and m was given then in such case T2cos2θ+T2sin2θ=(mg)2+(mRw2)2
T=√(mg)2+(mRw2)2 and use e=TlAy
Similar Questions
A stone of mass m is attached to one end of a wire of cross-sectional area A and Young's modulus Y. The stone is revolved in a horizontal circle at a speed such that the wire makes an angle θ with the vertical. The strain produced in the wire will be
06:28View Solutionm द्रव्यमान का एक पत्थर L लम्बाई के किसी तार के एक सिरे से बँधा है। तार का व्यास D है एवं इसे ऊर्ध्वाधर रूप से लटकाया जाता है। पत्थर अब क्षैतिज तल में घूमाया जाता हैं तथा तार ऊर्ध्वाधर से एक कोण θ बनाता है। यदि तार का यंग प्रत्यास्थता गुणांक Y है, तो तार की लम्बाई में वृद्धि होगी -
04:41View SolutionA metal wire of uniform cross-sectional area A and length L, has mass m. It is suspended vertically from a ceiling. If its Young's modulus is Y, then the elongation Δl of wire due to its own weight will be .........
05:52View SolutionAn object of mass m is suspended at the end of a massless wire of length L and area of cross -section A. Young modulus of the material of the wire is Y. If the mass is pulled down slightly its frequency of oscillation along the vertical direction is :
02:15View SolutionA wire of length I and radius of cross section is suspended vertically. If Y is Young.s madulus and d is density of the wire, find the increase in length of the wire due to its own weight .
View SolutionA block of mass Mis susended fom a wire of length L area of cross section A and Young.s modulus Y. Find the elastic potential energy stored in the wire.
View SolutionA stone of mass m is tied to one end of a wire of length L. The diameter of the wire is D and it is suspended vertically. The stone is now rotated in a horizontal plane and makes an angle θ with the vertical. If Young's modulus of the wire is Y, Then the increase in the length of the wire is
04:30View Solution

