An object of mass m is suspended at the end of a massless wire of length L and area of cross -section A. Young modulus of the material of the wire is Y. If the mass is pulled down slightly its frequency of oscillation along the vertical direction is :
f=12π√mLYA
f=12π√YAmL
f=12π√mAYL
f=12π√YLmA
To solve the problem of finding the frequency of oscillation of a mass suspended from a massless wire, we can follow these steps:
Step 1: Understand the Setup
We have a mass m suspended from a wire of length L and cross-sectional area A. The Young's modulus of the wire is Y. When the mass is pulled down slightly by a distance x, the wire stretches, and we need to analyze the forces involved.
Hint: Visualize the system and identify the forces acting on the mass when it is displaced.
Step 2: Determine the Stress and Strain in the Wire
When the mass is displaced by a distance x, the wire experiences a change in length. The stress σ in the wire can be expressed as:
σ=FA
where F is the force exerted by the mass (which is mg) and A is the cross-sectional area of the wire.
The strain ϵ in the wire is given by:
ϵ=ΔLL=xL
Hint: Recall the definitions of stress and strain, and how they relate through Young's modulus.
Step 3: Relate Stress and Strain Using Young's Modulus
According to Young's modulus Y:
Y=StressStrain=σϵ
Substituting the expressions for stress and strain, we have:
Y=F/Ax/L
Rearranging gives:
F=YAxL
Hint: Use the relationship F=kx for simple harmonic motion (SHM) where k is the spring constant.
Step 4: Identify the Restoring Force
The restoring force F acting on the mass when it is displaced by x is:
F=−YAxL
This indicates that the force is proportional to the displacement x and acts in the opposite direction, characteristic of SHM.
Hint: Recognize that the negative sign indicates a restoring force.
Step 5: Determine the Effective Spring Constant
From the expression for the restoring force, we can identify the effective spring constant k:
k=YAL
Hint: Relate the spring constant to the oscillation frequency.
Step 6: Calculate the Frequency of Oscillation
The frequency f of oscillation for a mass-spring system is given by:
f=12π√km
Substituting our expression for k:
f=12π√YAmL
Hint: Ensure that you understand the units and dimensions involved in the frequency formula.
Final Result
Thus, the frequency of oscillation of the mass is:
f=12π√YAmL
We have a mass m suspended from a wire of length L and cross-sectional area A. The Young's modulus of the wire is Y. When the mass is pulled down slightly by a distance x, the wire stretches, and we need to analyze the forces involved.
When the mass is displaced by a distance x, the wire experiences a change in length. The stress σ in the wire can be expressed as:
σ=FA
where F is the force exerted by the mass (which is mg) and A is the cross-sectional area of the wire.
ϵ=ΔLL=xL
According to Young's modulus Y:
Y=StressStrain=σϵ
Substituting the expressions for stress and strain, we have:
Y=F/Ax/L
Rearranging gives:
F=YAxL
The restoring force F acting on the mass when it is displaced by x is:
F=−YAxL
This indicates that the force is proportional to the displacement x and acts in the opposite direction, characteristic of SHM.
From the expression for the restoring force, we can identify the effective spring constant k:
k=YAL
The frequency f of oscillation for a mass-spring system is given by:
f=12π√km
Substituting our expression for k:
f=12π√YAmL
Thus, the frequency of oscillation of the mass is:
f=12π√YAmL
Topper's Solved these Questions
Similar Questions
A block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View SolutionA point mass m is suspended at the end of a massless wire of length l and cross section. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
View Solution
Knowledge Check
A wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
AYAx22LBYAx2L2CYAx2LDYAx2LA wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
AYLABYlACYALDYAl
A metal wire of length L, area of cross-section A and young's modulus Y is stretched by a variable force F such that F is always slightly greater than the elastic forces of resistance in the wire. When the elongation of the wire is l
View SolutionA load w is suspended from a wire of length l and area of cross-section A. Change in length of the wire is say Δl. Change in length Δl can be increased to two times by increasing
View SolutionA wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
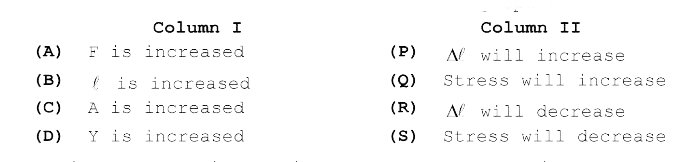
View SolutionThe length of a rod is 20cm and area of cross-section 2cm2. The Young's modulus of the material of wire is 1.4×1011N/m2. If the rod is compressed by 5kg−wt along its length, then increase in the energy of the rod in joules will be
View SolutionA wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View SolutionSpeed of transverse wave on a straight wire (mass m, length l , area of cross-section A) is. If the young’s modulus of wire is Y, the extension of wire over its natural length, is independent of
View Solution
