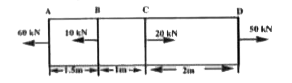
A steel rod of cross-sectional area $1 m^{2}$ is acted upon by forces shown in the fig. Determine the total elongation of the bar. Take $Y = 2.0 \times 10^{11} N / m^{2}$ .
Solution in Telugu

Video Solution

Text Solution

Verified by Experts

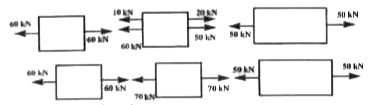
The action of forces on each part of rod is shown in fig.

We know that the extension due to external force F is given by $Δ_{A B} = \frac{F l}{A Y}$
$Δ l_{A B} = \frac{(60 \times 10^{3}) \times 1.5}{1 \times 2 \times 10^{11}} = 4.5 \times 10^{- 7} m$
$Δ l_{B C} = \frac{(70 \times 10^{3}) \times 1}{1 \times 2 \times 10^{11}} = 3.5 \times 10^{- 7} m$
and $Δ l_{C D} = \frac{(50 \times 10^{3}) \times 2}{1 \times 2 \times 10^{11}} = 5.0 \times 10^{- 7} m$
The total extension $Δ = Δ_{A B} + Δ_{B C} + Δ_{C D}$
$= 4.5 \times 10^{- 7} + 3.5 \times 10^{- 7} + 5.0 \times 10^{- 7} = 13 \times 10^{- 7} m$

|

Updated on:21/07/2023

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile