A sphere of radius R of material of refractive index μ3. Where should an object be placed so that a real image is formed equidistant from the sphere?

Let object be placed at a distance x from the pole P1 of the sphere then the ray must pass symmetrically through the sphere, as shown in the figure. Applying the equation at the first surface, we get
μ2−∞−μ1−x=μ2−μ1−Rorx=(μ1μ2−μ1)R
Note that the real image is formed only when the refractive index of the sphere is more than that of the surrounding i.e, μ2>μ1.
Topper's Solved these Questions
- RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE I
95 Videos
- RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE 1B
45 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
Similar Questions
A sphere of radius R made of material of refractive index μ2 is placed in a medium of refractive index μ1. Where would an object be placed so that a real image is formed at equidistant fromk the sphere? ltbgt
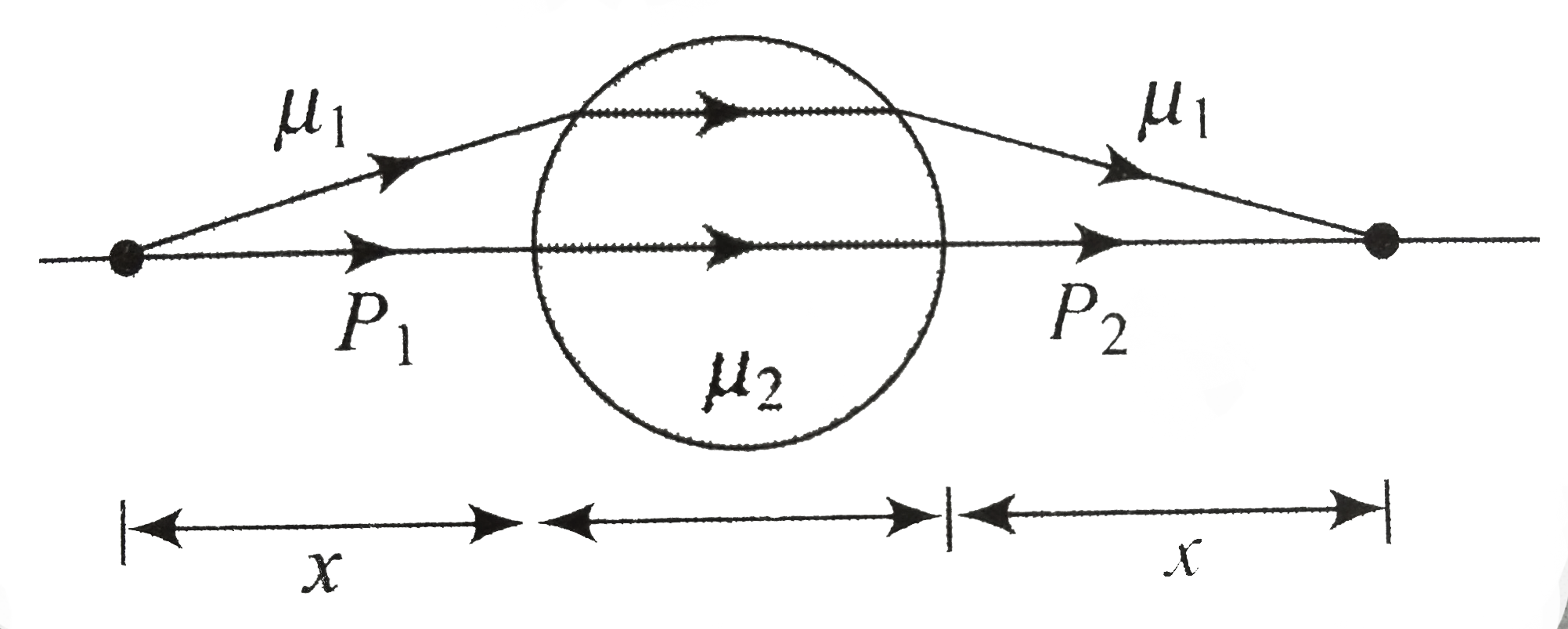
View SolutionA sphere of radius R made of material of refractive index μ2 is placed in a medium of refractive index μ1. Where would an object be placed so that a real image is formed at equidistant fromk the sphere? ltbgt

View Solution
Knowledge Check
There is a sphere of radius R and refractive index μ. At what distance from the surface of sphere should an object be placed so that real image is formed at the same distance from the sphere ?
ARμ−1BRμCR2−μD2Rμ−1A transparent sphere of radius R and refractie index μ is kept in air. At what distance from the surface of the sphere shold a point object be placed so as to form a rea image at the same distance from the sphere?
AR/μBμRCRμ−1DRμ+1The figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.

If x=2R,then the value of μisA1.5B2C3Dnone of these
The figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.

If x=2R,then the value of μis
View SolutionThe figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
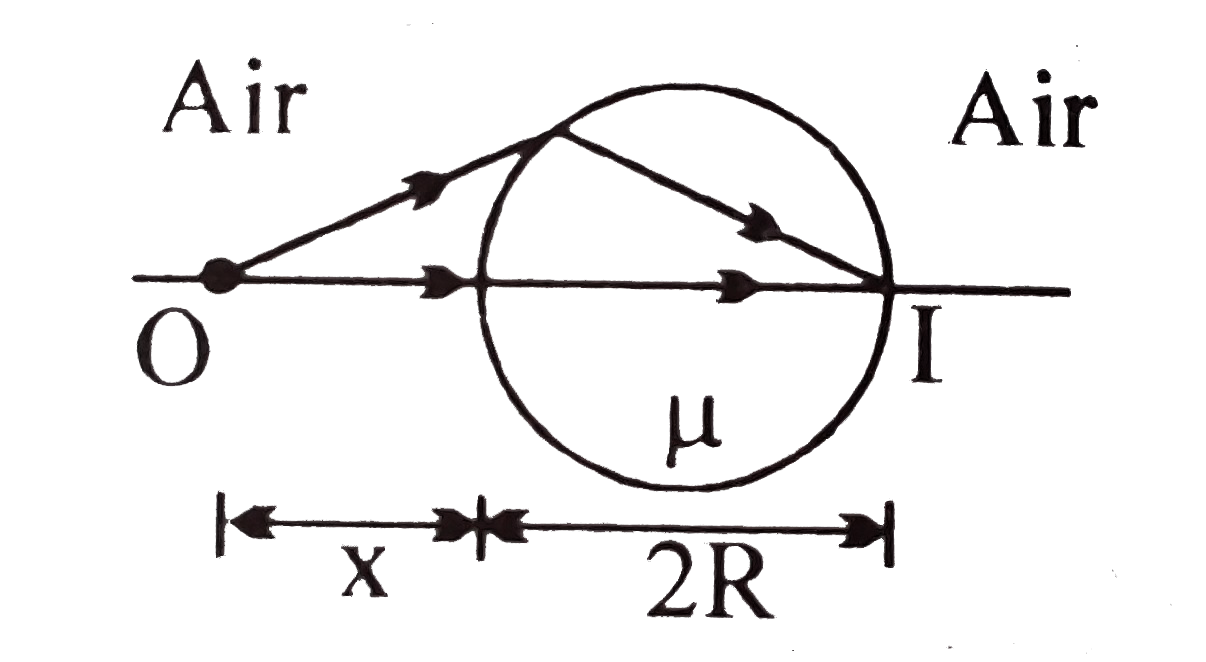 If x=∞,then the value of μ is
If x=∞,then the value of μ is
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
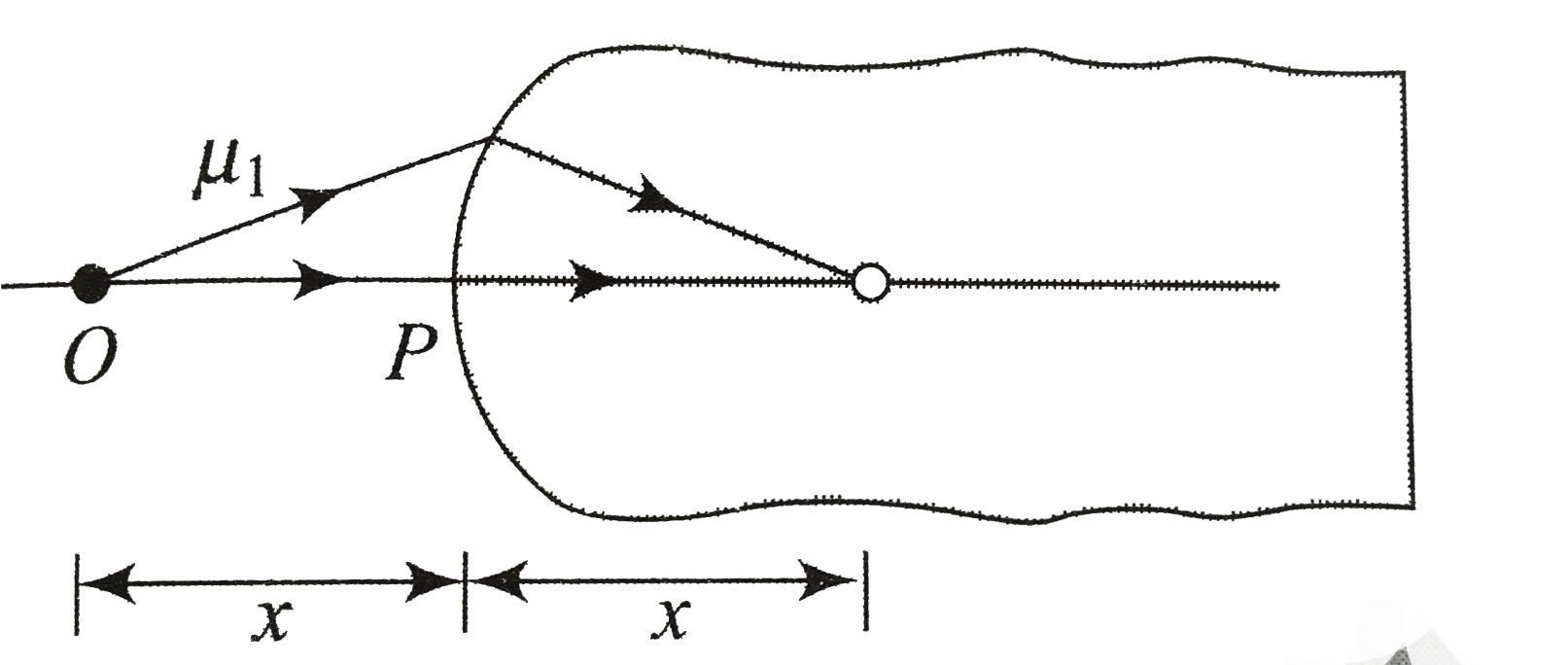
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?

View SolutionThe figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
 If x=∞,then the value of μ is
If x=∞,then the value of μ is
View Solution
