A small plane mirror is rotating at a constant frequency of n rotation per second. With what linear velocity will a light spot move along a spherical screen of radius of curvature of R metres if the mirror at the centre of curvature of the screen?
4πnR
2πnR
πnR
4nR
The correct Answer is:A
Topper's Solved these Questions
- RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE II
113 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
Similar Questions
A small plane mirror is rotating at constant frequency of n rotations per second. With what linear velocity (in ms-1) will a light spot move along a spherical screen of radius of curvature of R metres if the mirror is at the centre of curvature of the screen?
View SolutionA flat mirror revolves at a constant angular velocity making n=0.4 revolutions per second. With what velocity (in m s−1) will a light spot move along a spherical screen with a radius of 15 m, if the mirror is at the centre of curvature of the screen ?
View Solution
Knowledge Check
A flat mirror revolves at a constant angular velocity making n=0.4 revolutions per second. With what velocity (in m s−1) will a light spot move along a spherical screen with a radius of 15 m, if the mirror is at the centre of curvature of the screen ?
A37.7B60.3C68.7D75.4If the frequency of a rotating platform is v and the distance of a boy from the centre is r, what is the area swept out per second by the line connecting the boy to the centre?
AπrυB2πrυCπr2υD2πr2υThe separation between the screen and a concave mirror is 2 r . An isotropic point source of light is placed exactly midway between the mirror and the point source. Mirror has a radius of curvature r and reflects 100% of the incident light. Then the ratio of illuminances on the screen with and without the mirror is
A10:1B2:1C10:9D9:1
Figure shows a plane mirror hinged at O and free to rotate in a vertical plane. The point O is at a distance x from a long screen. A beam of light moving vertically downwards is reflected by the mirror at O so that a bright spot P is formed at the screen. At the instant shown, the angle of incidence is θ and the mirror is rotating clockwise with constant angular veloity ω. Find the speed of spot P at this instant.
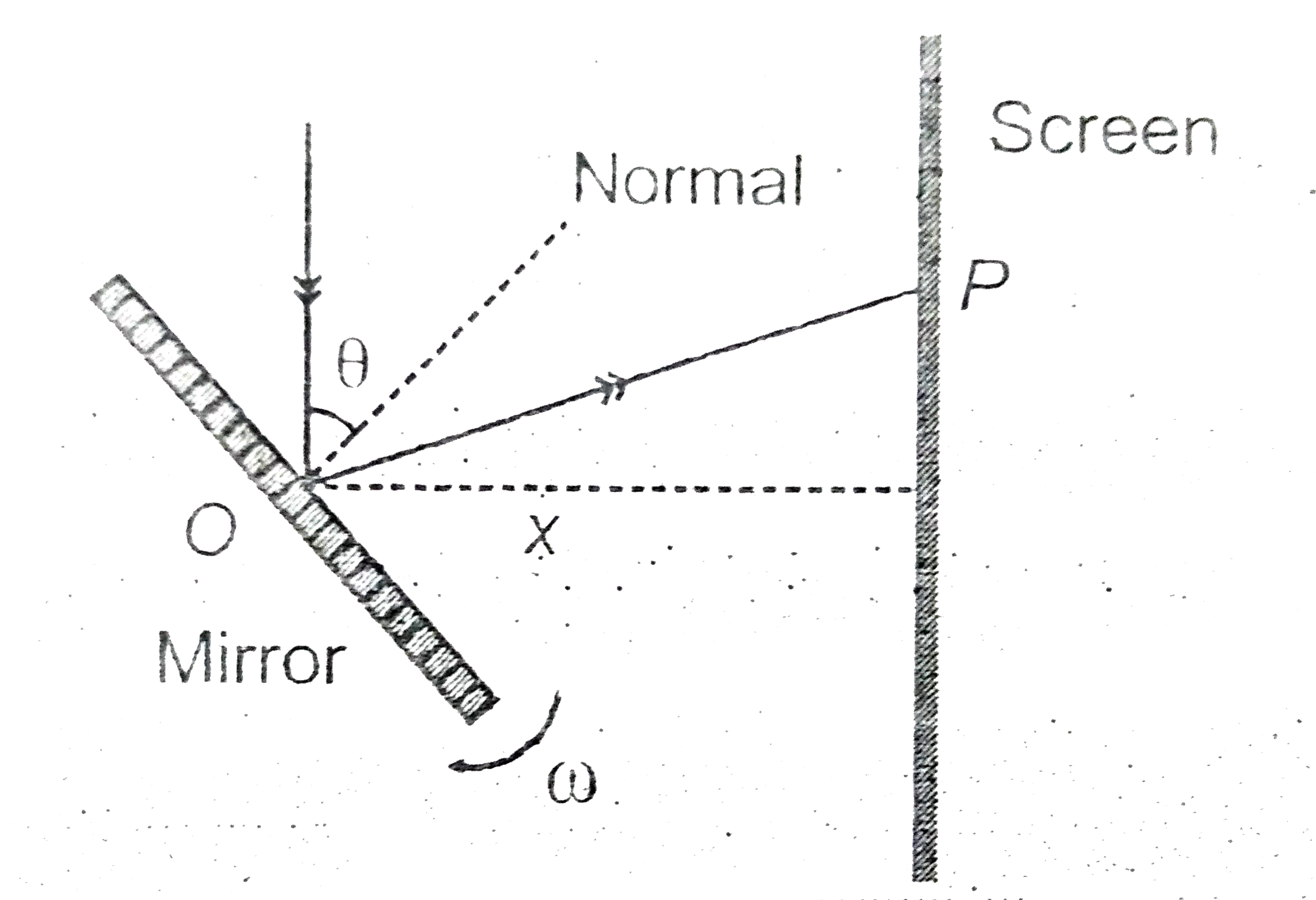
View SolutionFigure shows a plane mirror hinged at O and free to rotate in a vertical plane. The point O is at a distance x from a long screen. A beam of light moving vertically downwards is reflected by the mirror at O so that a bright spot P is formed at the screen. At the instant shown, the angle of incidence is θ and the mirror is rotating clockwise with constant angular veloity ω. Find the speed of spot P at this instant.

View SolutionAn electron moving in a circular orbit of radius makes n rotations per second. The magnetic field produced at the centre has magnitude :
View SolutionAn electron moving in a circular orbit of radius r makes n rotation per second. The magnetic field produced at the centre has magnitude
View SolutionA small plane mirror kept at the centre of a sphere of diameter 3 m, makes 12 revolution per second. A thin light beam is made incident on the mirror. The linear speed of the light spot on the sphere, formed after reflection-from the mirror is:
View Solution
