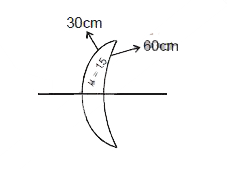
A thin equi-convex lens having radius of curvature 10cm is placed as shown in figure . Calculate the focal length of the lens, if parallel rays are incident as shown
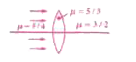
Refraction at 1st surface u=∞,μ1=54μ2=53
μ2v−μ1u=μ2−μ1R1⇒53v=53−5410⇒v=40cm
Refraction at second surface
μ1=53,μ2=32μ=+40v=?R=−10
32v−53×40=32−53−10 After solving we get V=1807cm
So focal length =1807cm
Topper's Solved these Questions
- RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE I
95 Videos
- RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE 1B
45 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
Similar Questions
Knowledge Check
A thin equi-convex lens having radius of curvature 10 cm is placed as shown in figure. Calculate focal length of the lens, if parallel rays are incident as shown.
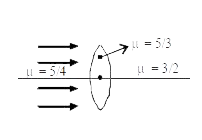 A1207 cmB1607 cmC1807 cmDNone
A1207 cmB1607 cmC1807 cmDNoneA plano-convex lens has refractive index 1.6 and radius of curvature 60 cm. What is the focal length of the lens?
A50 cmB100 cmC200 cmD150 cm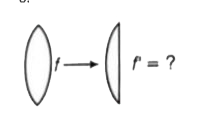
If the bio-convex lens is cut as shown in the figure, the new focal length f' isA2fBfC(f)/(2)DInfinite
If in a plano-convex lens, the radius of curvature of the convex surface is 10 cm and the focal length of the lens is 30 cm , then the refractive index of the material of lens will be
View SolutionIf in a plano-convex lens, the radius of curvature of the convex surface is 10 cm and the focal length of the lens is 30 cm , then the refractive index of the material of lens will be
View SolutionIf in a plano-convex lens, the radius curvature of the convex surface is 10 cm and the focal length of the lens is 30 cm, then the refractive index of the material of lens will be
View SolutionIf in a plano-convex lens, the radius curvature of the convex surface is 10 cm and the focal length of the lens is 20 cm , then the refractive index of the material of lens will be
View SolutionThe radius of curvature of the convex surface of a planoconvex lens is 12 cm and its refractive index 1.5. If the plane face of the lens is silvered, then the distance from the lens at which parallel rays incident on its convex surface converge is
View Solution