Question

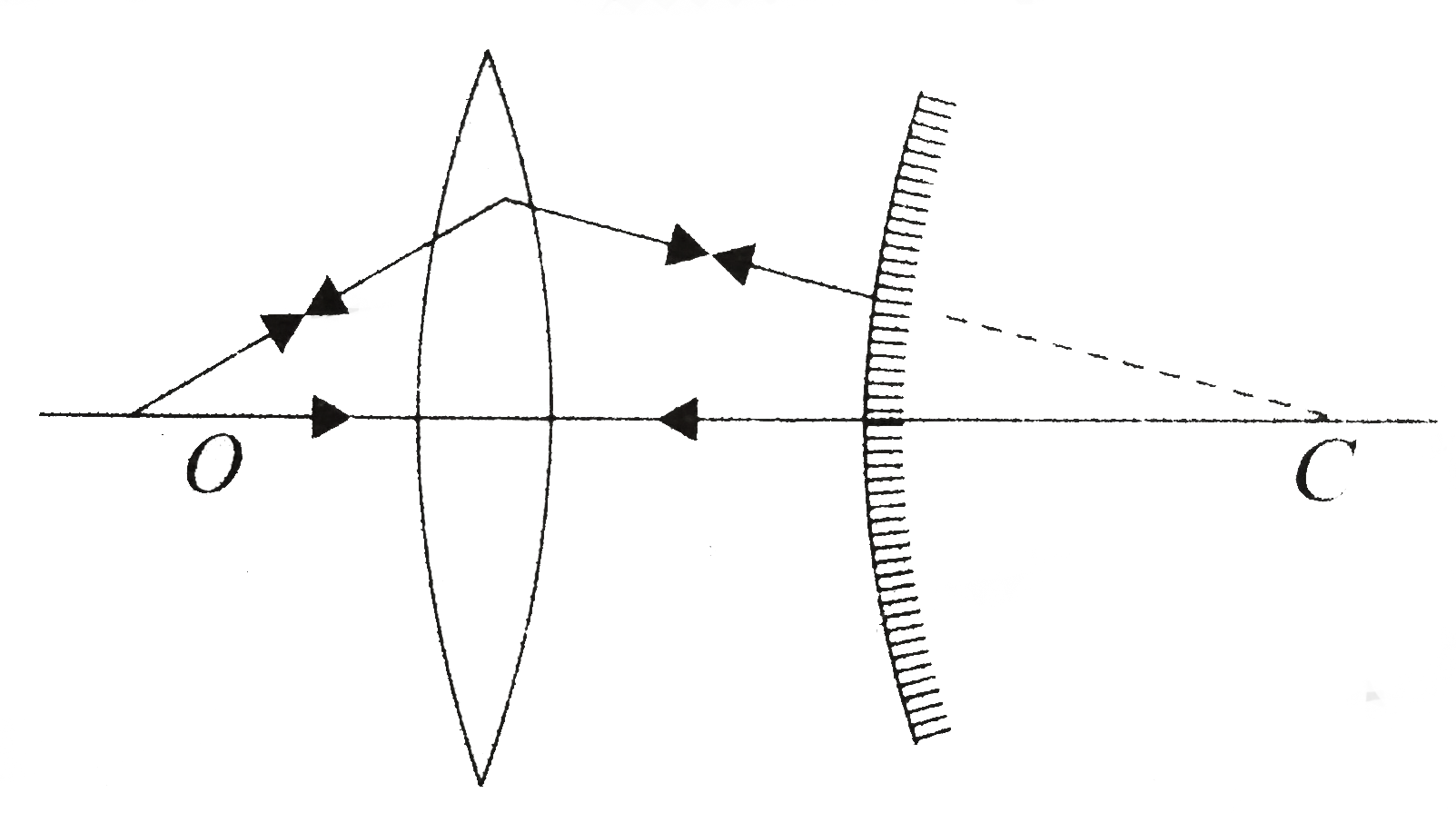
A point object is placed at a distance of 12cm on the axis of a convex lens of focal length 10cm . On the other side of the lens, a convex mirror is placed at a distance of 10cm from the lens such that the image formed by the combination coincides with the object itself. What is the focal length of convex mirror?

Explanation

For convex lens `1/v-1/(-12)=1/10`
i.e., v=60 cm i.e., in the absence of convex mirror. Convex lens will form the image `I_1` at a distance of 60cm behind the lens. Since the mirror is at a distance of 10cm from the lens `I_1` will be at a distance of 60-10=50 cm from the mirror, i.e., `MI_1=50 cm`

Now as the final image `I_2` s formed at the object O itself, the rays after reflection from the mirror retraces its path i.e., rays on the mirror are incident normallly i.e., `I_1` is the centre of the mirror , so that `R=MI_1=50 cm and ` hence `F=(R//2)=(50//2)=25 cm`