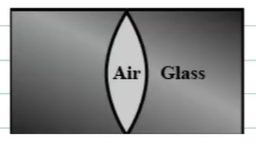
As shown in figure a spherical air lens of radii $R_{1} = R_{2} = 10 c m$ is cut in a glass cylinder. Determine the focal length and nature of air lens. IF a liquid of refractive index 2 is filled in the lens, what will happens to its focal length and nature?
$As shown in figure a spherical air lens of radii R1=R2=10cm is cut in a glass cylinder. Determine the focal length and nature of air lens. IF a liquid of refractive index 2 is filled in the lens, what will happens to its focal length and nature?$

Text Solution

Verified by Experts

According to lens maker formula,
$\frac{1}{f} = (μ - 1) [\frac{1}{R_{1}} - \frac{1}{R_{2}}]$ with $μ = \frac{μ_{1}}{μ_{2}}$ Intially
$μ = \frac{μ_{a}}{μ_{u}} = \frac{1}{(3 / 2)} = \frac{2}{3}, R = + 10 c m and R_{2} = - 10 c m$
So $\frac{1}{f} = [\frac{2}{3} - 1] [\frac{1}{+ 10} - \frac{1}{- 10}] = - \frac{2}{30} i . e ., f = - 15 c m$
i.e. the air lens in glass behaves as divergent lens of focal length 15 cm
When the liquid of $μ = 2$ is filled in the air cavity.
$μ = \frac{μ_{1}}{μ_{u}} = \frac{2}{1.5} = \frac{4}{3}$ So that now $\frac{1}{f} . = [\frac{4}{3} - 1] [\frac{1}{10} - \frac{1}{10}] = \frac{2}{30}$
f.=15cm i.e., the liquid lens in glass will behaves as a convergent lens of focal length 15cm.

Updated on:21/07/2023

A lens of refractive index n is put in a liquid of refractive index $n'$ . If focal length of lens in air is $f$ , its focal length in liquid will be.
A $\frac{f n' (n - 1)}{n' - n}$
B $\frac{f (n' - 1)}{n' (n - 1)}$
C $\frac{n' (n - 1)}{f (n' - 1)}$
D $\frac{f n' n}{n - n'}$
A lens of refractive index n is put in a liquid of refractive index $n'$ . If focal length of lens in air is $f$ , its focal length in liquid will be.
A $\frac{- f n' (n - 1)}{n' - n}$
B $\frac{- f (n' - n)}{n' (n - 1)}$
C $\frac{- n' (n - 1)}{f (n' - n)}$
D $\frac{f n' n}{n - n'}$
In the figure, an air lens is cut a cylinder of glass of refractive index 1.5 . The nature of the lens is

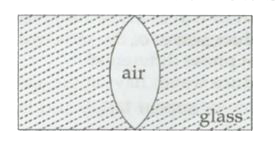Adiveriging
Bconverging
Cneither diverging nor converging
Dnone of these