If all the three interaxial angles defining the unit ceil are equal in magnitude, the crystal cannot be!ong to
(I) Orthorhombic system
(II) Monoclinic system
(III) Hexagonal system
(IV) Tetragonal system
II, III
I, IV
III, IV
I, II
The correct Answer is:A
To solve the question, we need to analyze the interaxial angles of the different crystal systems mentioned: Orthorhombic, Monoclinic, Hexagonal, and Tetragonal.
Step 1: Understand the Interaxial Angles
The interaxial angles (α, β, γ) define the geometry of the unit cell in crystal systems:
- Orthorhombic system: α = β = γ = 90°
- Monoclinic system: α = γ = 90°, β ≠ 90°
- Hexagonal system: α = β = 90°, γ = 120°
- Tetragonal system: α = β = γ = 90°
Step 2: Identify the Condition
The question states that all three interaxial angles are equal in magnitude. This means we are looking for a system where α = β = γ.
Step 3: Analyze Each System
1. Orthorhombic: All angles are equal (90°). This system can have equal angles.
2. Monoclinic: Two angles are equal (90°), but one is not. This system cannot have all three angles equal.
3. Hexagonal: Two angles are equal (90°), and one is 120°. This system cannot have all three angles equal.
4. Tetragonal: All angles are equal (90°). This system can have equal angles.
Step 4: Conclusion
From the analysis, the Monoclinic and Hexagonal systems cannot have all three angles equal. However, the question asks for the system that cannot belong to the condition of all angles being equal.
Since the Monoclinic system is the only one where two angles are equal and one is not, it is the correct answer.
Final Answer
The crystal cannot belong to the Monoclinic system.
---
The interaxial angles (α, β, γ) define the geometry of the unit cell in crystal systems:
- Orthorhombic system: α = β = γ = 90°
- Monoclinic system: α = γ = 90°, β ≠ 90°
- Hexagonal system: α = β = 90°, γ = 120°
- Tetragonal system: α = β = γ = 90°
The question states that all three interaxial angles are equal in magnitude. This means we are looking for a system where α = β = γ.
1. Orthorhombic: All angles are equal (90°). This system can have equal angles.
2. Monoclinic: Two angles are equal (90°), but one is not. This system cannot have all three angles equal.
3. Hexagonal: Two angles are equal (90°), and one is 120°. This system cannot have all three angles equal.
4. Tetragonal: All angles are equal (90°). This system can have equal angles.
From the analysis, the Monoclinic and Hexagonal systems cannot have all three angles equal. However, the question asks for the system that cannot belong to the condition of all angles being equal.
The crystal cannot belong to the Monoclinic system.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If all three iterfacial angeles defining the unit cell, are equal in magniture, the crystal cannot be:
ArhombohedralBcubicChexagonalDtetragonalThe magnitude of electrostatic unit of charge in S.I. system is
A1.602×10−19CB9.1×10−31CC3×108CD3×10−19CTetragonal crystal system has the following unit cell dimensions :
Aa=b=c,α=β=γ=90∘Ba=b≠c,α=β=γ=90∘Ca≠b≠c,α=β=γ=90∘Da=b≠c,α=β=90∘γ=120∘
Tetragonal crystal system has the following unit cell dimensions:
View SolutionTetragonal crystal system has the following unit cell dimensions :
View SolutionTetragonal crystal system has the following unit cell dimensions :
View SolutionWhich of the crystal systems has all the axial angles equal but not equal to 90∘?
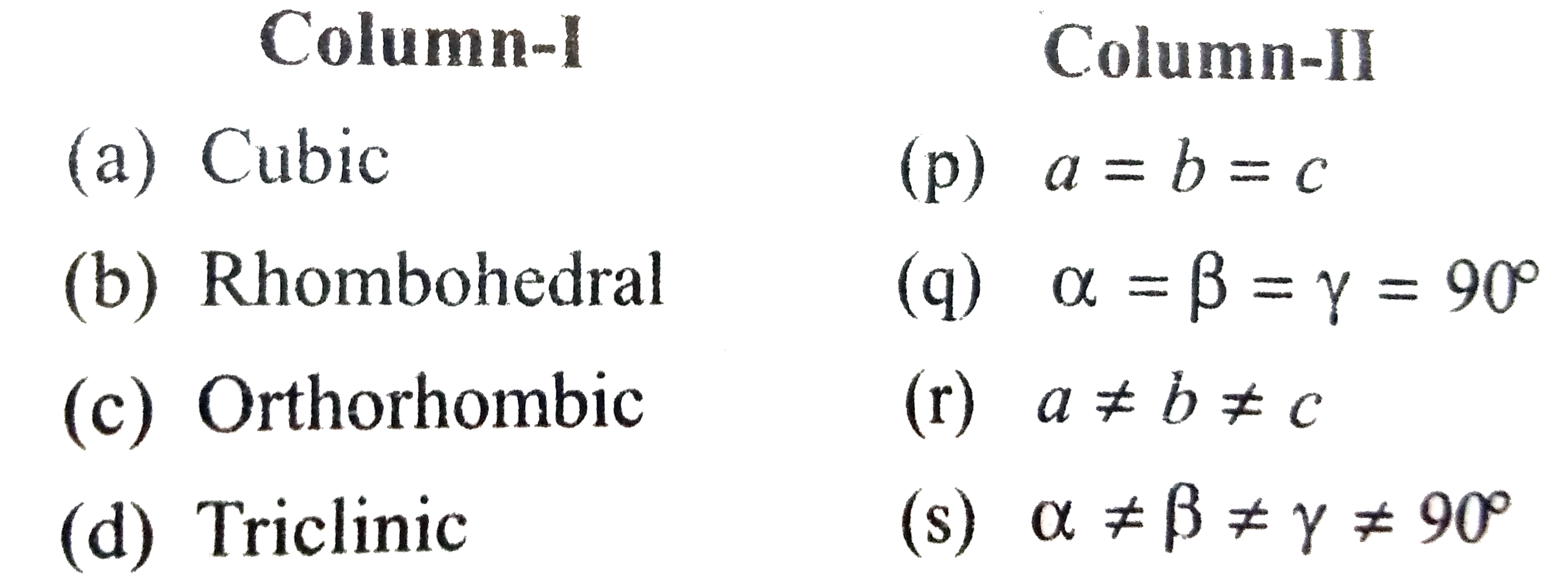
View SolutionMatch the crystal system (column I) with its characteristics (column II)

View Solution