A rod of mass M and length L is made to stand vertically. Potential energy of the rod in this position is
Mgl
Mgl2
Mgl3
Mgl4
The correct Answer is:B
To find the potential energy of a vertically standing rod of mass M and length L, we can follow these steps:
1. Identify the Center of Mass:
The center of mass of a uniform rod is located at its midpoint. For a rod of length L, the center of mass is at a distance of L2 from either end.
2. Determine the Height of the Center of Mass:
When the rod is standing vertically, the center of mass is at a height of L2 above the ground.
3. Calculate the Potential Energy:
The potential energy (PE) of an object at height h is given by the formula:
PE=mgh
where:
- m is the mass of the object,
- g is the acceleration due to gravity (approximately 9.81m/s2),
- h is the height above the reference point (ground level in this case).
4. Substituting Values:
In our case, the mass of the rod is M and the height h is L2. Therefore, the potential energy of the rod when it is standing vertically is:
PE=M⋅g⋅L2
5. Final Expression:
Thus, the potential energy of the rod in the vertical position is:
PE=MgL2
Final Answer:
The potential energy of the rod in the vertical position is MgL2.
---
The center of mass of a uniform rod is located at its midpoint. For a rod of length L, the center of mass is at a distance of L2 from either end.
When the rod is standing vertically, the center of mass is at a height of L2 above the ground.
The potential energy (PE) of an object at height h is given by the formula:
PE=mgh
where:
- m is the mass of the object,
- g is the acceleration due to gravity (approximately 9.81m/s2),
- h is the height above the reference point (ground level in this case).
In our case, the mass of the rod is M and the height h is L2. Therefore, the potential energy of the rod when it is standing vertically is:
PE=M⋅g⋅L2
Thus, the potential energy of the rod in the vertical position is:
PE=MgL2
The potential energy of the rod in the vertical position is MgL2.
Topper's Solved these Questions
Similar Questions
A uniform rod of mass M and length L is standing vertically along the y-axis on a smooth horizontal surface as shown. A small disturbance causes the lower end to slip on the smooth horizontal surface and rod starts falling. The path followed by centre of mass of the rod during the fall is

View SolutionA uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View Solution
Knowledge Check
A rod of mass m and length / is made to stand at an angle of 60∘ with the vertical. Potential energy of the rod in this position is
AmglBmgl2Cmgl3Dmgl4A uniform rod of mas m and length l is made to stand at an angle of 60∘ with the vertical. What is the potential energy of the rod in this position?
AmglBmgl2Cmgl3Dmgl4A thin homogeneous rod of mass m and length l is free to rotate in vertical plane about a horizontal axle pivoted at one end of the rod. A small ballof mass m and charge q is attached to the opposite end of this rod. The whole system is positioned in a horizontal electric field of magnitude E=mg2q. The rod is released from, shown position from rest.

What is the speed of ball when rod becomes vertical?A√2gl3B√3gl4C√3gl2D√4gl3
A uniform slender rod of mass M and length L is pivoted at its end. The rod is released from its nearly vertical position. What is the reaction at the pivot when the rod reaches the horizontal position? If the support is withdrawn at this instant, describe the subsequent motion of the rod.
View SolutionA horizontal metallic rod of mass m and length l is supported by two vertical identical springs of spring constant k each and natral length i0 A current l is flowing in the rod in the direction shown if the rod is in equilibrium then the length of each spring in this state is:
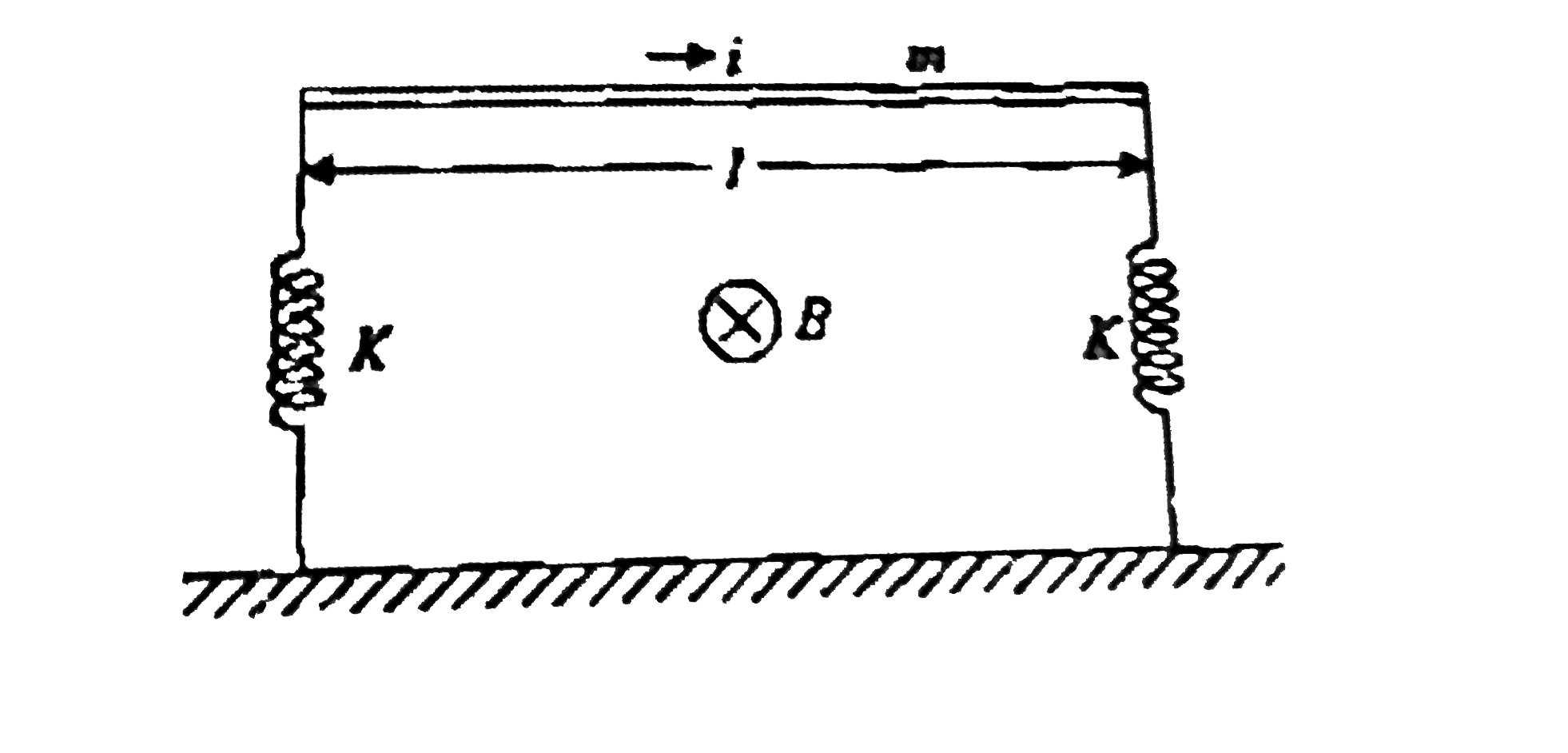
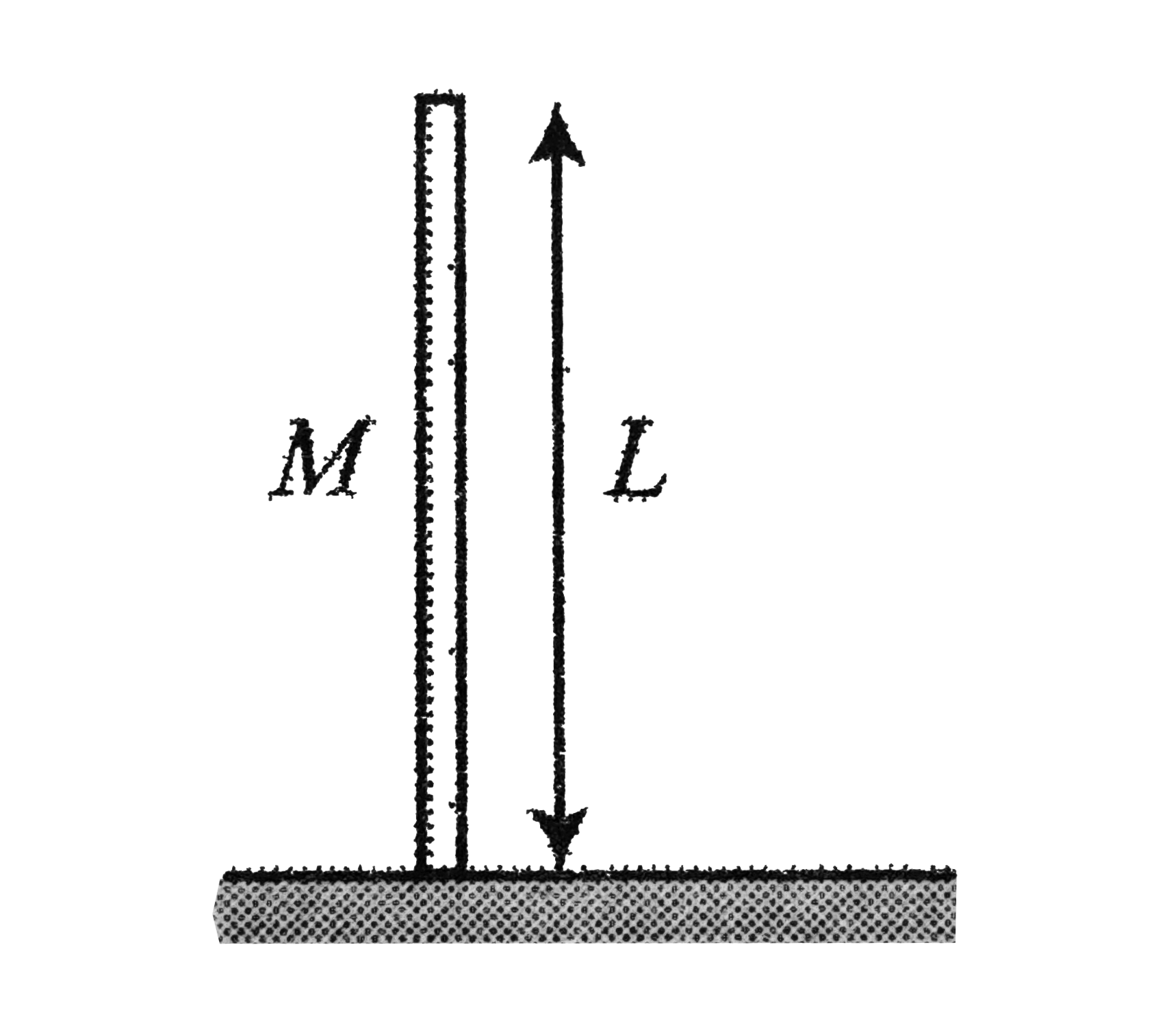
View SolutionA uniform rod of mass M and length L is held vertically upright on a horizontal surface as shown in figure. Assuming zero potential energy at the base of the rod, determine the potential energy of the rod.
View SolutionA thin homogeneous rod of mass m and length l is free to rotate in vertical plane about a horizontal axle pivoted at one end of the rod. A small ballof mass m and charge q is attached to the opposite end of this rod. The whole system is positioned in a horizontal electric field of magnitude E=mg2q. The rod is released from, shown position from rest.

What is the angular acceleration of the rod at the instant of releasing the rod?
View SolutionA rod of length L and mass m is kept vertically on the ground. Its potential energy is :
View Solution
