Two masses 6 kg and 4 kg are connected by massless flexible and inextensible string passing over massless and frictionless pulley.The acceleration of centre of mass is (g=10ms^2)
0.4ms−2
2ms−2
50ms−2
Zero
The correct Answer is:A
To find the acceleration of the center of mass of the system consisting of two masses (6 kg and 4 kg) connected by a massless string over a frictionless pulley, we can follow these steps:
Step 1: Identify the masses and gravitational acceleration
Let:
- m1=6kg (mass 1)
- m2=4kg (mass 2)
- g=10m/s2 (acceleration due to gravity)
Step 2: Calculate the net force acting on the system
The net force (F) acting on the system can be calculated as the difference in weight of the two masses:
F=m1g−m2g=(6kg⋅10m/s2)−(4kg⋅10m/s2)
F=60N−40N=20N
Step 3: Calculate the total mass of the system
The total mass (M) of the system is the sum of the two masses:
M=m1+m2=6kg+4kg=10kg
Step 4: Calculate the acceleration of the system
Using Newton's second law (F=Ma), we can find the acceleration (a) of the system:
a=FM=20N10kg=2m/s2
Step 5: Calculate the acceleration of the center of mass
The acceleration of the center of mass (acm) can be calculated using the formula:
acm=m1a1+m2a2m1+m2
Since both masses have the same acceleration (equal to the acceleration of the system), we can use a1=a2=a:
acm=m1a+m2am1+m2=(m1+m2)am1+m2=a
Thus, the acceleration of the center of mass is:
acm=2m/s2
Final Answer:
The acceleration of the center of mass is 2m/s2.
---
Let:
- m1=6kg (mass 1)
- m2=4kg (mass 2)
- g=10m/s2 (acceleration due to gravity)
The net force (F) acting on the system can be calculated as the difference in weight of the two masses:
F=m1g−m2g=(6kg⋅10m/s2)−(4kg⋅10m/s2)
F=60N−40N=20N
The total mass (M) of the system is the sum of the two masses:
M=m1+m2=6kg+4kg=10kg
Using Newton's second law (F=Ma), we can find the acceleration (a) of the system:
a=FM=20N10kg=2m/s2
The acceleration of the center of mass (acm) can be calculated using the formula:
acm=m1a1+m2a2m1+m2
Since both masses have the same acceleration (equal to the acceleration of the system), we can use a1=a2=a:
acm=m1a+m2am1+m2=(m1+m2)am1+m2=a
Thus, the acceleration of the center of mass is:
acm=2m/s2
The acceleration of the center of mass is 2m/s2.
Topper's Solved these Questions
Similar Questions
Two masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
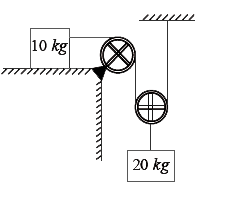
View SolutionTwo masses 8 kg and 12 kg are connected at the two ends of a light inextensible string that passes over a frictionless pulley Fibd the acceleration of the masses and tension in the string , when the masses are released
 .
.
View Solution
Knowledge Check
Two masses m and m (m>m) are connected by massless flexible and inextensible string passed over massless and frictionless pulley. The acceleration of centre of mass is
A(m1−m2m1+m2)2gBm1−m2m1+m2gCm1+m2m1−m2gDZeroTwo bodies of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
A4.9m/s2B2.45m/s2C1.4m/s2D9.5m/s2Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two masses 7 kg and 12 kg are connected at the two ends of a light inetensible string that goes over a frictionless pulley. Find the acceleration of the masses and the tension in the string when the masses are released.
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
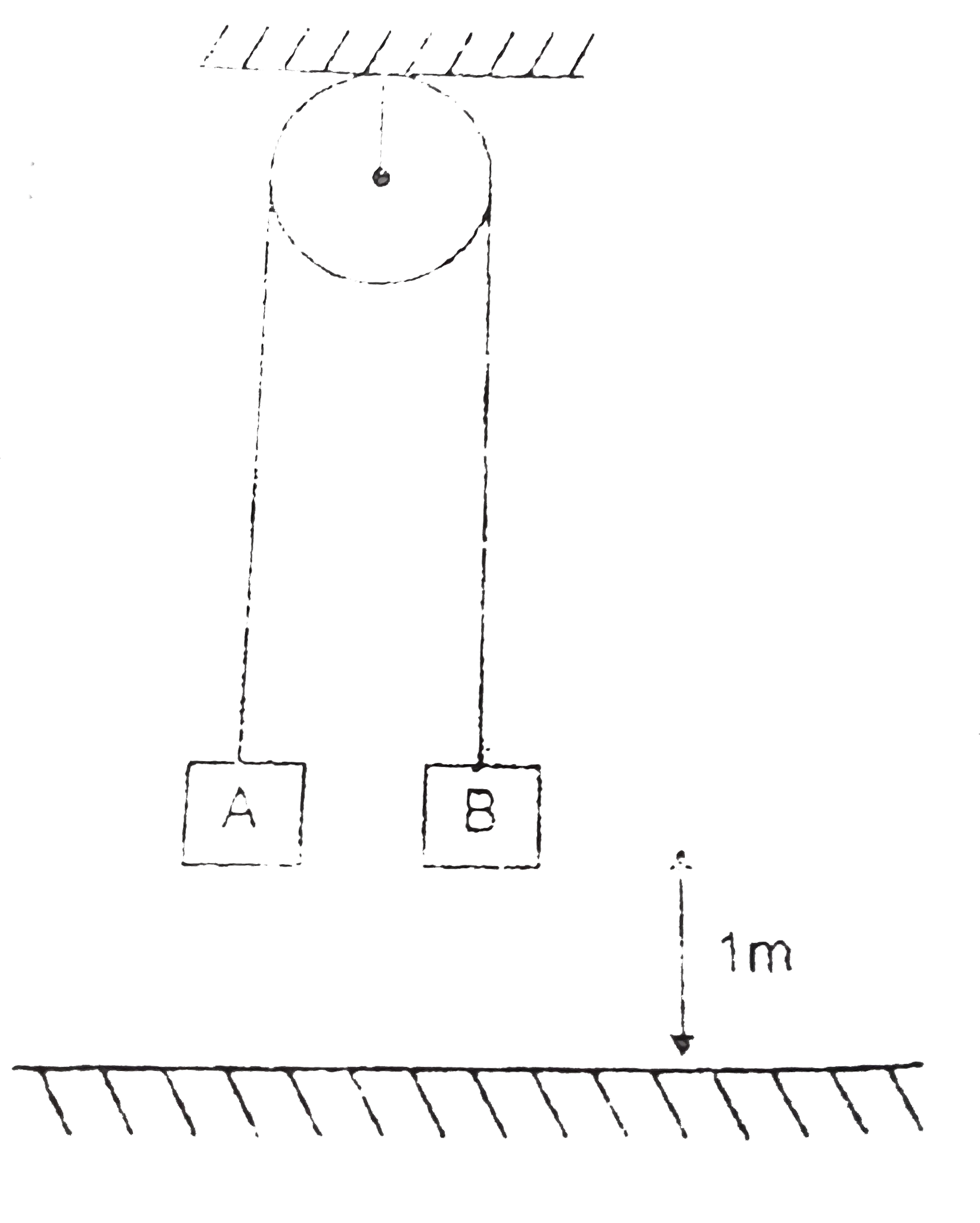
View SolutionTwo masses A and B of 3kg and 2kg are connected by a long inextensible string which passes over a massless and frictionless pulley. Initially the height of both the masses from the ground is same and equal to 1 metre. When the masses are released. Mass A hits the ground and gets stuck to the ground. Consider the length of the string as large, so that the pulley does not obstruct the motion of masses A and B [g=10m/s2]
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo masses of 10 kg and 6 kg connected at the two ends of an inextensible string pass over a smooth frictionless pulley . Calculate acceleration of the system and tension in the string .
View Solution
