which of the following equation is incorrect for a body undergoing rotational motion with uniform angular acceleration ( symbols have their usual meanings)

A

$ω = ω_{0} + α t$

B

theta - theta_0 = omega_0t + 1/2alphat^2

C

$ω^{2} - ω_{0}^{2} = α (θ - θ_{0})$

D

$ω^{2} - ω_{0}^{2} = 2 α (θ - θ_{0})$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:C

To determine which equation is incorrect for a body undergoing rotational motion with uniform angular acceleration, we can analyze the equations provided and compare them to their linear motion counterparts.
1. Identify the equations for rotational motion:
- The equations for a body in rotational motion with uniform angular acceleration are analogous to those in linear motion. The standard equations are:
1. $ω = ω_{0} + α t$
2. $θ - θ_{0} = ω_{0} t + \frac{1}{2} α t^{2}$
3. $ω^{2} - ω_{0}^{2} = 2 α (θ - θ_{0})$
2. Analyze each equation:
- Equation 1: $ω = ω_{0} + α t$
- This equation is correct. It states that the final angular velocity ( $ω$ ) is equal to the initial angular velocity ( $ω_{0}$ ) plus the product of angular acceleration ( $α$ ) and time ( $t$ ).

- Equation 2: $θ - θ_{0} = ω_{0} t + \frac{1}{2} α t^{2}$
- This equation is also correct. It represents the angular displacement ( $θ - θ_{0}$ ) in terms of initial angular velocity, angular acceleration, and time.

- Equation 3: $ω^{2} - ω_{0}^{2} = 2 α (θ - θ_{0})$
- This equation is incorrect as stated. The correct form should be $ω^{2} - ω_{0}^{2} = 2 α (θ - θ_{0})$ , but the way it is presented in the question suggests that there is a misunderstanding in the formulation. The correct interpretation should not include the extra term or misplacement of factors.
3. Conclusion:
- The incorrect equation among the options provided is the third one, which is presented as $ω^{2} - ω_{0}^{2} = 2 α (θ - θ_{0})$ but may have been misrepresented in the question context.
Final Answer:
The incorrect equation for a body undergoing rotational motion with uniform angular acceleration is:
Option C: $ω^{2} - ω_{0}^{2} = 2 α (θ - θ_{0})$ .

Updated on:18/9/2024

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

The correct combination is (symbols have their usual meanings)

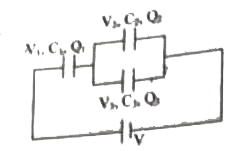A $Q_{1} = Q_{2} = Q_{3} and V_{1} = V_{2} = V_{3} = V$
B $Q_{1} = Q_{2} + Q_{3} and V = V_{1} + V_{2} + V_{3}$
C $Q_{1} = Q_{2} + Q_{3} and V = V_{1} + V_{2}$
D $Q_{2} = Q_{3} and V_{2} = V_{3}$
Select the incorrect relation. (Where symboles have their usual meanings):-
A $C_{p} = \frac{γ R}{γ - 1}$
B $C_{P} - C_{V} = R$
C $Δ U = \frac{P_{f} V_{f} - P_{i} V_{i}}{1 - γ}$
D $C_{v} = \frac{R}{γ - 1}$
Bohr magnetonis given by (symbols have their usual meanings)
A $\frac{4 π m_{e}}{e h^{2}}$
B $\frac{4 π m_{e}}{e h}$
C $\frac{e h^{2}}{4 π m_{e}}$
D $\frac{e h}{4 π m_{e}}$

AAKASH INSTITUTE-MOCK TEST 11-Example

Home
Ask Doubt
Profile