the angular acceleration of flywheel having moment of inertia 50 kg when a torque of 5 is applied on the flywheel is
The correct Answer is:A
To find the angular acceleration of the flywheel, we can use the relationship between torque, moment of inertia, and angular acceleration. The formula we will use is:
τ=I⋅α
Where:
- τ is the torque applied (in N·m),
- I is the moment of inertia (in kg·m²),
- α is the angular acceleration (in rad/s²).
1. Identify the given values:
- Moment of inertia, I=50kg⋅m2
- Torque, τ=5N⋅m
2. Rearrange the formula to solve for angular acceleration (α):
α=τI
3. Substitute the known values into the equation:
α=5N⋅m50kg⋅m2
4. Perform the calculation:
α=550=0.1rad/s2
5. State the final answer:
The angular acceleration of the flywheel is 0.1rad/s2.
- τ is the torque applied (in N·m),
- I is the moment of inertia (in kg·m²),
- α is the angular acceleration (in rad/s²).
- Moment of inertia, I=50kg⋅m2
- Torque, τ=5N⋅m
α=τI
α=5N⋅m50kg⋅m2
α=550=0.1rad/s2
The angular acceleration of the flywheel is 0.1rad/s2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The angular momentum of a flywheel having a moment of inertia of 0.4kgm2 decreases from 30 to 20 kgm2/s in a period of 2 second. The average torque acting on the flywheel during this period is :
A10 N.mB2 . 5 N.mC5 N.mD1 . 5 N.mThe angular speed of a flywheel rotating at 90 r.p.m . Is
Aπ rad/sB2π rad/sC4π rad/sD3π rad/sCalculate the angular acceleration if a flywheel gains a speed of 540 r.p.m. in 6 seconds.
A3πrads−2B6πrads−2C9πrads−2D12πrads−2
A cord of negligible mass is wound round the rim of a flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
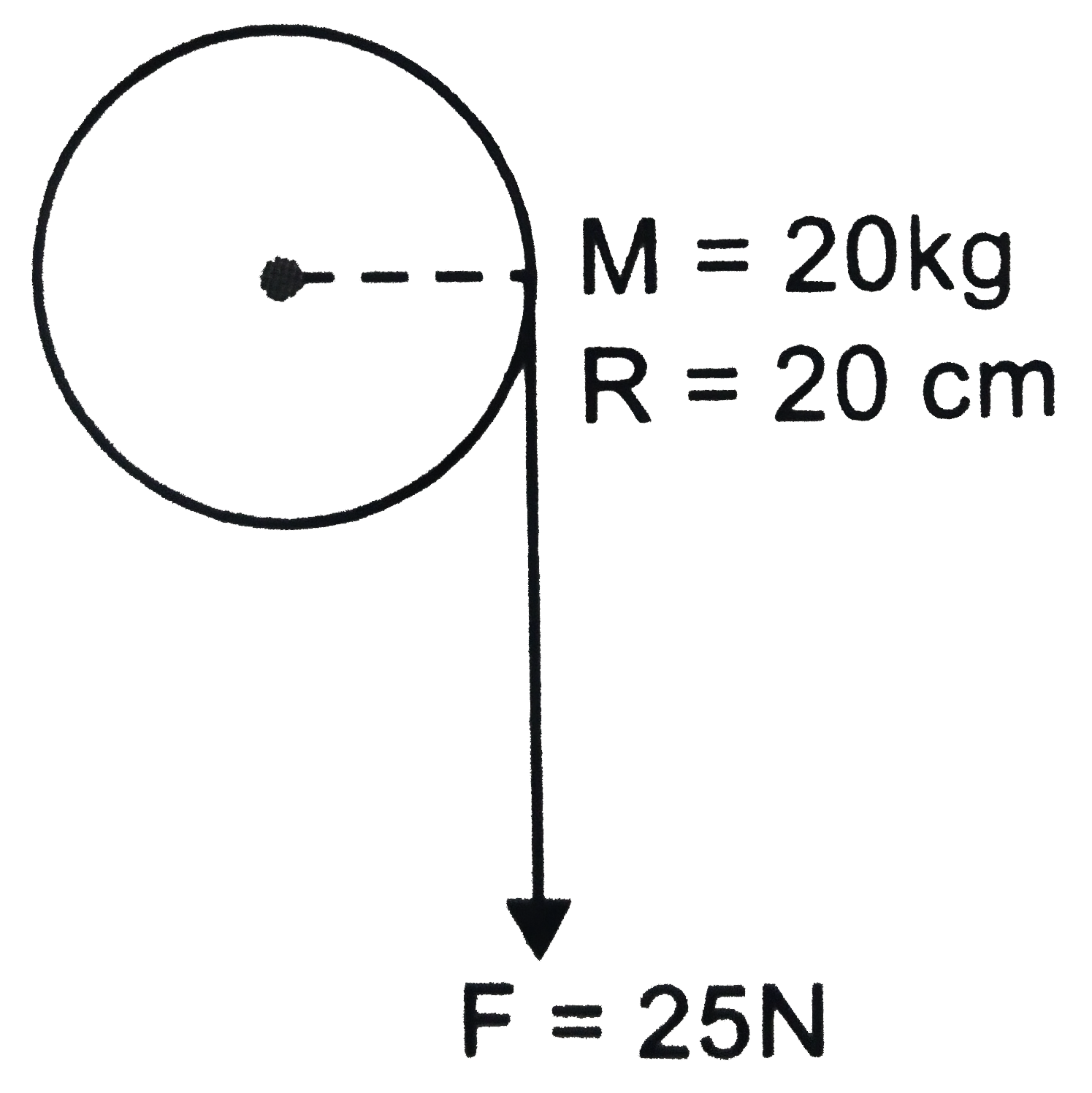
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View SolutionA flywheel has moment of inertia 4kg−m2 and has kinetic energy of 200 J. Calculate the number of revolutions it makes before coming to rest if a constant opposing couple of 5N-m is applied to the flywheel
View SolutionA 50 N m torque acts on a wheel with a moment of inertia 150kg⋅m2. If the wheel starts from rest, how long will it take the wheel to make 1 rev?
View SolutionThe moment of inertia of a solid flywheel about its axis is 0.1kg−m2.A tangential force of 2 kg-wt. is applied round the circumference of the flywheel with the help of a string and mass arrangement as shown in the figure. If the radius of the wheel is 0.1 m, find the acceleration (in rad/sec2) of the mass :
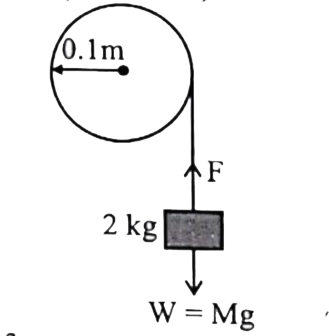
View SolutionThe torque needed to produce an angular acceleration of 18rad/sec2 in a body of moment of inertia 2.5kg-m2 would be -
View Solution
