A particle of mass m and charge -q circulates around a fixed charge q in a circle radius under electrostatic force. The total energy of the system is (k= (14πε0))
−Kq22r
Kq2r
−Kq2r
Zero
The correct Answer is:A
To solve the problem, we need to find the total energy of a system where a particle of mass m and charge −q is circulating around a fixed charge q in a circular path of radius r under the influence of electrostatic forces.
1. Identify the Forces Acting on the Particle:
The particle with charge −q experiences an electrostatic force due to the fixed charge q. This force provides the necessary centripetal force for the circular motion of the particle.
2. Write the Expression for Electrostatic Force:
The electrostatic force F between the two charges is given by Coulomb's law:
F=k⋅|q⋅(−q)|r2=kq2r2
where k=14πϵ0.
3. Set Up the Centripetal Force Equation:
The centripetal force required to keep the particle moving in a circle is given by:
Fc=mv2r
where v is the speed of the particle.
4. Equate the Electrostatic Force to the Centripetal Force:
Since the electrostatic force provides the centripetal force, we can set them equal:
kq2r2=mv2r
5. Solve for Velocity v:
Rearranging the equation gives:
mv2=kq2r
Thus,
v2=kq2mr
6. Calculate the Kinetic Energy KE:
The kinetic energy of the particle is given by:
KE=12mv2=12m(kq2mr)=kq22r
7. Calculate the Potential Energy PE:
The potential energy U of the system due to the electrostatic interaction is given by:
U=k⋅q⋅(−q)r=−kq2r
8. Find the Total Energy E:
The total energy E of the system is the sum of the kinetic energy and potential energy:
E=KE+PE=kq22r−kq2r
Simplifying this gives:
E=kq22r−2kq22r=−kq22r
9. Final Answer:
Therefore, the total energy of the system is:
E=−kq22r
Conclusion:
The total energy of the system is −kq22r, which corresponds to option 1 in the provided choices.
The particle with charge −q experiences an electrostatic force due to the fixed charge q. This force provides the necessary centripetal force for the circular motion of the particle.
The electrostatic force F between the two charges is given by Coulomb's law:
F=k⋅|q⋅(−q)|r2=kq2r2
where k=14πϵ0.
The centripetal force required to keep the particle moving in a circle is given by:
Fc=mv2r
where v is the speed of the particle.
Since the electrostatic force provides the centripetal force, we can set them equal:
kq2r2=mv2r
Rearranging the equation gives:
mv2=kq2r
Thus,
v2=kq2mr
The kinetic energy of the particle is given by:
KE=12mv2=12m(kq2mr)=kq22r
The potential energy U of the system due to the electrostatic interaction is given by:
U=k⋅q⋅(−q)r=−kq2r
The total energy E of the system is the sum of the kinetic energy and potential energy:
E=KE+PE=kq22r−kq2r
Simplifying this gives:
E=kq22r−2kq22r=−kq22r
Therefore, the total energy of the system is:
E=−kq22r
The total energy of the system is −kq22r, which corresponds to option 1 in the provided choices.
Topper's Solved these Questions
Similar Questions
A particle of mass m carrying charge '+q1' is revolving around a fixed charge '−q2' in a circular path of radius r. Calculate the period of revolution.
View SolutionA particle of mass m carrying a charge −q1 starts moving around a fixed charge +q2 along a circulare path of radius r. Find the time period of revolution T of charge −q1.
View Solution
Knowledge Check
Three charged particle sare in equilibrium under their electrostatic forces only. Then
Athe particle smust be collinearBall the charges cannot have the same magnitudeCall the charges cannot have the same signDthe equilibrium is unstableOn rotating a point charge g around a charge Q in a circle of radius r, the work done is
Aq.2πrBq.2πOrCzeroDQ2ε0rTwo charges q1 and q2 are placed 30 cm apart, as shown in the figure. A third charge q, is moved along the arc of a circle of radius 40 cm from C to D. The change in the potential energy of system is kq34πε0, then the value of k is
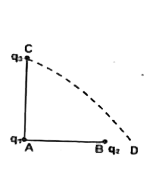 A8q2B8q1C6q2D6q1
A8q2B8q1C6q2D6q1
Two charges +qand−q, each of mass m, are revoloving in a circle of radius R, under mutal electrostatic force, Find (i) speed of each charge (ii) kinitic energy of the system (iii) potental energy of the system and (iv) total energy of the system.
View SolutionA particle of mass m and carrying charge −q1 is moving around a charge +q2 along a circular path of radius r. Period of revolution of the charge −q1 about +q2 is
View SolutionA particle of mass m and charge -q moves diametrically through a uniformily charged sphere of radius R with total charge Q. The angular frequency of the particle's simple harminic motion, if its amplitude lt R, is given by
View SolutionTwo point charges q each are fixed at (a,0) and (-a,0). A third charge Q is placed at origin. Electrons potential energy of the system will
View SolutionTwo charges q1 and q2 are placed 30cm apart, as shown in the figure. A third charge q3 is moved along the arc of a circle of radius 40cm from C to D. The change in the potential energy o fthe system is q34πε0k., where k is
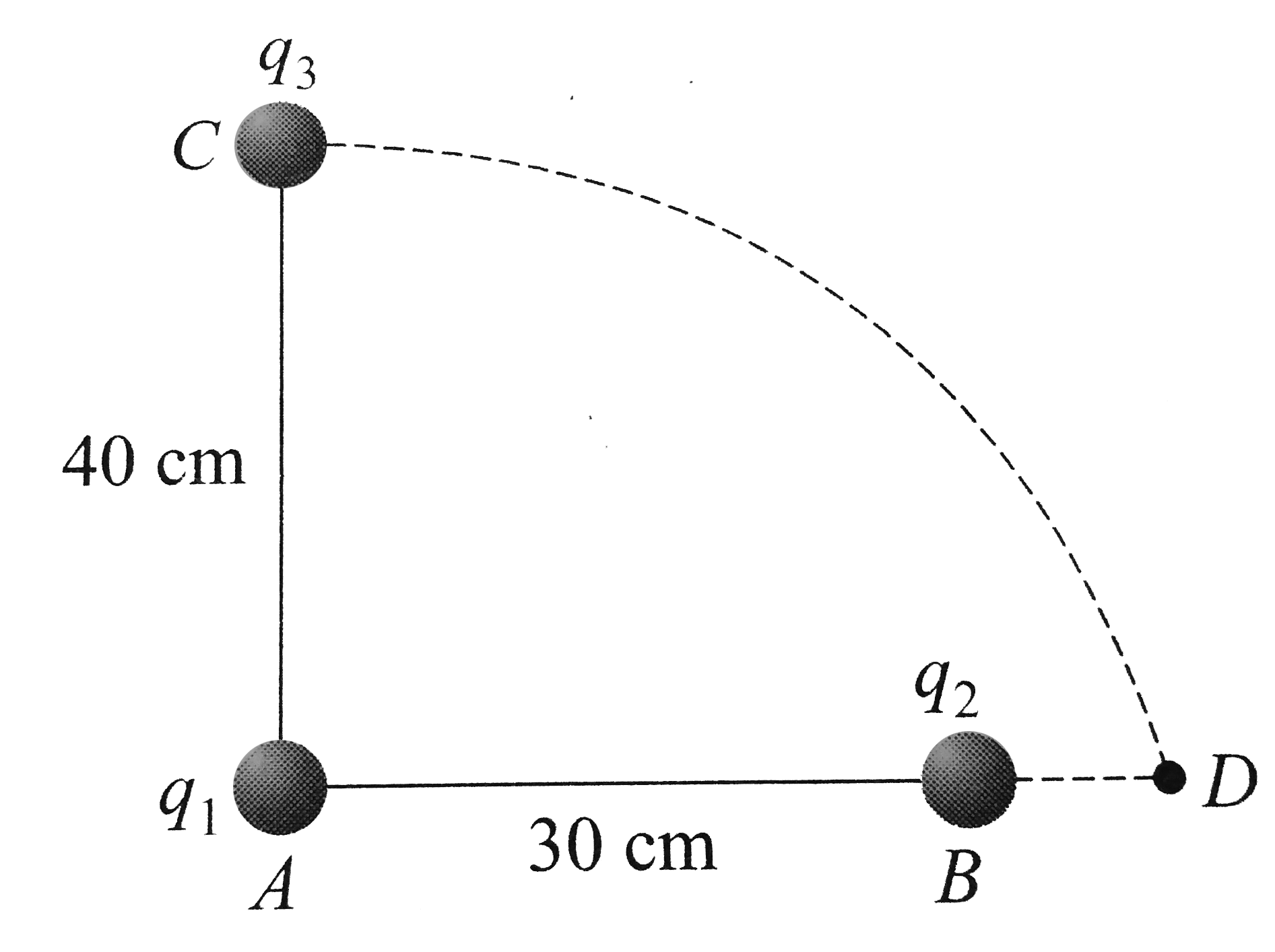
View Solution
