A parallel plate capacitor is filled with a uniform dielectric , maximum charge that can be given to it does not depends upon
Dielectric constant of the dielectric
Dielectric strenth of the dielectric
Separation between the plates
Area of the plates
The correct Answer is:C
To solve the question regarding the maximum charge that can be given to a parallel plate capacitor filled with a uniform dielectric, we need to analyze the factors that influence this maximum charge.
1. Understanding the Capacitor with Dielectric:
A parallel plate capacitor consists of two plates separated by a distance, and when a dielectric material is introduced between the plates, it affects the capacitor's ability to store charge.
2. Dielectric Constant (k):
The dielectric constant (k) is a measure of how much the dielectric material reduces the electric field within the capacitor. It is a crucial factor in determining the capacitance of the capacitor when a dielectric is present.
3. Capacitance with Dielectric:
The capacitance (C) of a parallel plate capacitor filled with a dielectric is given by:
C=kϵ0Ad
where:
- ϵ0 is the permittivity of free space,
- A is the area of the plates,
- d is the separation between the plates.
4. Maximum Charge (Q):
The maximum charge (Q) that can be stored in the capacitor is given by:
Q=C⋅V
where V is the voltage across the capacitor. Substituting the expression for capacitance, we have:
Q=kϵ0Ad⋅V
5. Factors Affecting Maximum Charge:
From the equation Q=kϵ0Ad⋅V, we can see that the maximum charge depends on:
- The dielectric constant (k),
- The area of the plates (A),
- The voltage (V),
- The separation between the plates (d).
6. Identifying the Independent Factor:
The question asks for the factor that does not affect the maximum charge. Among the factors listed, the maximum charge does not depend on the separation (d) of the plates. This is because, while the capacitance is inversely proportional to the separation, the maximum charge is influenced by the voltage applied, which can be adjusted independently of the separation.
Conclusion:
Thus, the maximum charge that can be given to a parallel plate capacitor filled with a uniform dielectric does not depend on the separation between the plates.
Final Answer:
The maximum charge that can be given to the capacitor does not depend on the separation of the plates (d).
---
A parallel plate capacitor consists of two plates separated by a distance, and when a dielectric material is introduced between the plates, it affects the capacitor's ability to store charge.
The dielectric constant (k) is a measure of how much the dielectric material reduces the electric field within the capacitor. It is a crucial factor in determining the capacitance of the capacitor when a dielectric is present.
The capacitance (C) of a parallel plate capacitor filled with a dielectric is given by:
C=kϵ0Ad
where:
- ϵ0 is the permittivity of free space,
- A is the area of the plates,
- d is the separation between the plates.
The maximum charge (Q) that can be stored in the capacitor is given by:
Q=C⋅V
where V is the voltage across the capacitor. Substituting the expression for capacitance, we have:
Q=kϵ0Ad⋅V
From the equation Q=kϵ0Ad⋅V, we can see that the maximum charge depends on:
- The dielectric constant (k),
- The area of the plates (A),
- The voltage (V),
- The separation between the plates (d).
The question asks for the factor that does not affect the maximum charge. Among the factors listed, the maximum charge does not depend on the separation (d) of the plates. This is because, while the capacitance is inversely proportional to the separation, the maximum charge is influenced by the voltage applied, which can be adjusted independently of the separation.
Thus, the maximum charge that can be given to a parallel plate capacitor filled with a uniform dielectric does not depend on the separation between the plates.
The maximum charge that can be given to the capacitor does not depend on the separation of the plates (d).
Topper's Solved these Questions
Similar Questions
Knowledge Check
A parallel plate capacitor is filled with dielectrics. What is capacitance?
 A2K1K2K1+K2BK1K2K1+K2C2ε0Ad(K1K2K1+K2)D2ε0Ad(2K1+K22K1K2)
A2K1K2K1+K2BK1K2K1+K2C2ε0Ad(K1K2K1+K2)D2ε0Ad(2K1+K22K1K2)The capacitance of a capacitor does not depend upon
Aeither charge Q or potential VBarea of either platesCdistance between the platesDnature of medium between the platesSpace between the plates of a parallel plate capacitor is filled with a dielectric slab. The capacitor is charged and then the supply is disconnected to it. If the slab is now taken out then
Awork is not done to take out the slabBenergy stored in the capacitor reducesCpotential difference across the capacitor is decreasedDpotential difference across the capacitor is increased
A parallel-plate capacitor is filled with a delectric meterial having resistivity(ρ)and dielectric constant K.The capcitor is charged and disconnected from the charging source. The capacitor is slowly discharged through the dielectric.Show that the time constant of the discharge is independent of all gepmetrical parameters like the plate area or separation between the plates. Find this time constant.
View SolutionIf the gap between the plates of a parallel plate capacitor is filled with medium of dielectric constant k=2 , then the field between them
View SolutionIn figure half of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?

View SolutionThe space between plates of a parallel plate capacitor is filled by a dielectric and it is charged and then battery is removed. Now dielectric slab is slowly drawn out of the capacitor parallel to the plates. The variatiton of the potential of capacitor with respect to the length of the dielectric plate drawn out is
View SolutionA parallel-plate capacitor is filled with a dielectric upto one-half of the distance between the plates. The manner in which, the potential between the plates varies is illustrated in the figure
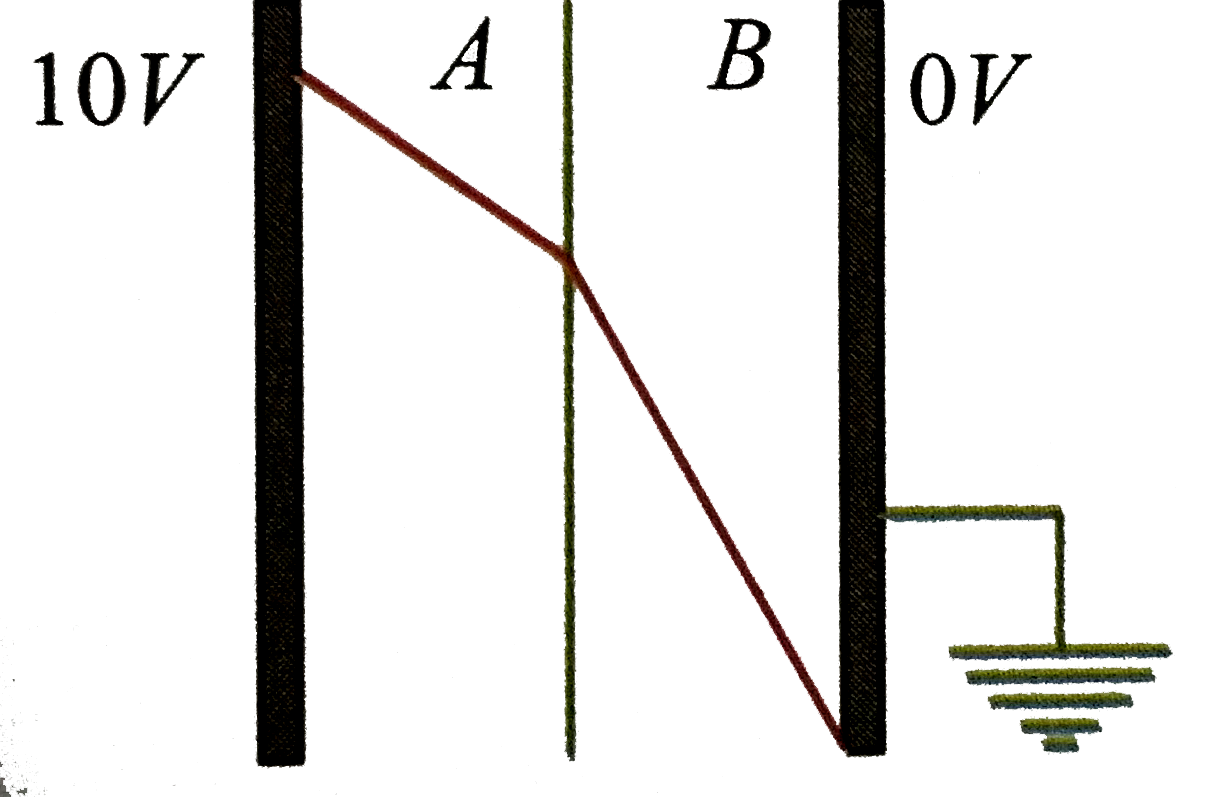 .
.
View Solution

