If a equiconvex lens of focal length f is cut into two halves by a plane perpendicular to the principal axis, then
The focal length of each half becomes
The focal length of each half becomes 2f
The focal length of each half remains f
The focal length of each half becomes f4
The correct Answer is:B
To solve the problem of finding the focal length of each half of an equiconvex lens after it has been cut into two halves by a plane perpendicular to the principal axis, we can follow these steps:
Step 1: Understand the Lens Properties
An equiconvex lens has equal radii of curvature on both sides. Let the focal length of the original lens be f. The lens maker's formula is given by:
1f=μ(1r1−1r2)
where:
- μ is the refractive index of the lens material,
- r1 and r2 are the radii of curvature of the two surfaces of the lens.
For an equiconvex lens, we have r1=r and r2=−r (the negative sign indicates that the second surface is convex towards the incoming light).
Step 2: Apply the Lens Maker's Formula
Substituting the values into the lens maker's formula, we get:
1f=μ(1r−(−1r))=μ(1r+1r)=μ(2r)
Thus, we can express the focal length as:
1f=2μr
Step 3: Cut the Lens in Half
When the lens is cut into two halves by a plane perpendicular to the principal axis, we need to analyze one of the halves. For one half of the lens:
- One surface remains with radius of curvature r.
- The other surface becomes flat (infinite radius of curvature), hence r2=∞.
Step 4: Apply the Lens Maker's Formula Again
Now, applying the lens maker's formula for the half lens, we have:
1f′=μ(1r−1∞)=μ(1r−0)=μr
Step 5: Relate the Focal Lengths
From the previous steps, we have:
1f′=μr
We know from the earlier step that 1f=2μr. Therefore, we can relate f′ to f:
1f′=12⋅1f
This implies:
f′=2f
Conclusion
The focal length of each half of the lens after being cut is 2f.
An equiconvex lens has equal radii of curvature on both sides. Let the focal length of the original lens be f. The lens maker's formula is given by:
- μ is the refractive index of the lens material,
- r1 and r2 are the radii of curvature of the two surfaces of the lens.
Substituting the values into the lens maker's formula, we get:
When the lens is cut into two halves by a plane perpendicular to the principal axis, we need to analyze one of the halves. For one half of the lens:
- One surface remains with radius of curvature r.
- The other surface becomes flat (infinite radius of curvature), hence r2=∞.
Now, applying the lens maker's formula for the half lens, we have:
From the previous steps, we have:
The focal length of each half of the lens after being cut is 2f.
Topper's Solved these Questions
Similar Questions
An equi-convex lens of focal length F in air is is cut into two halves along the plane perpendicular to the optic axis. One of the halves is placed between a fixed object and a screen separated by distance of 90 cm . Two images are formed on the screen for two different positions of the lens with magnification 2 and 1/2 respectively. Find the value of F . what would be the value of the focal length of the equiconvex lens if the lens is immersed in water ? Refractive index of the material of the lens is 1.5 and that of water is μw=4/3.
View SolutionAn extended object of size 2mm is placed on the principal axis of a converging lens of focal length 10cm. It is found that when the object is placed perpendicular to the principal axis the image formed is 4mm in size. The size of image when it is placed along the principal axis is ____________ mm.
View Solution
Knowledge Check
An equiconvex lens of glass of focal length 0.1 metre is cut along a plane perpendicular to principle axis into two equal parts. The ratio of focal length of new lenses formed is:
A1:1B1:2C2:1D2:12An equiconvex lens of glass of focal length 0.1 meter is cut along a plane perpendicular to principle axis into two equal parts. The ratio of focal length of new lenses forms is
A1:1B1:2C2:1D2:12If a symmetrical convex lens of focal length 'f is cut into two parts along the principal axis as shown in the figure, the focal length of each part will be:
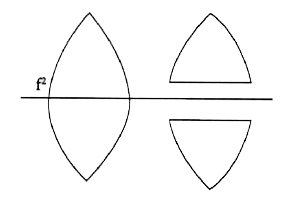 Af2Bf4CfD∞
Af2Bf4CfD∞
A symmetric double convex lens is cut in two equal parts by a plane perpendicular to the principal axis. If the power of the original lens is 4D, the power of a cut lens will be
View SolutionA symmetric double convex lens is cut in two equal parts by a plane perpendicular to the principal axis. If the power of the original lens is 4D, the power of a cut lens will be
View SolutionThere is a convex lens of focal length 20 cm. An object of height 3 cm is placed perpendicular to principal axis of lens at a distance 10 cm from the lens. Find the size of image.
View SolutionA symmetric double convex lens is cut in two equal parts by a plane perpendicular to the principal axis. If the power of the original lens was 4D, the power of a cut lens will be
View SolutionThe two surfaces of a biconvex lens has same radii of curvatures . This lens is made of glass of refractive index 1.5 and has a focal length of 10 cm in air. The lens is cut into two equal halves along a plane perpendicular to its principal axis to yield two plane - convex lenses. The two pieces are glued such that the convex surfaces touch each other. If this combination lens is immersed in water (refractive index =43 ), its focal length (in cm ) is
View Solution