Determine whether the f(x)=sinx function is strictly monotonic on the indicated interval.
(0,2π)Solution in Malayalam
Step by step video & image solution for Determine whether the f(x)=sinx function is strictly monotonic on the indicated interval. (0,2pi) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Consider the following figure
find the point of intersection (P) of the parabola and the line.
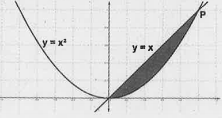
View SolutionFind the intervals of monotonicities and hence find the local extremum for the following functions:
f(x)=sinxcosx+5,x∈(0,2π)
View SolutionVerify Rolle's Theorem for the functions :
f(x)=sinx+cosx in the interval [0,2π]
View SolutionDetermine the intervals in which the following functions are strictly increasing or strictly decreasing :
f(x)=(x−1)(x−2)2.
View SolutionDetermine the intervals of monotonicity for the following functions :
f(x)=ln|x|,
View SolutionDetermine the intervals of monotonicity for the following functions :
f(x)=ex+5x
View SolutionDetermine whether the f(x)=x2 function is strictly monotonic on the indicated interval.
(−1,1)
View SolutionDetermine whether the f(x)=x2 function is strictly monotonic on the indicated interval.
(−1,0)
View SolutionDetermine whether the f(x)=x2 function is strictly monotonic on the indicated interval.
(0,1)
View SolutionDetermine whether the f(x)=x3−x function is strictly monotonic on the indicated interval.
(−1,0)
View SolutionDetermine whether the f(x)=x3−x function is strictly monotonic on the indicated interval.
(−1,−12)
View SolutionDetermine whether the f(x)=x3−x function is strictly monotonic on the indicated interval.
(−1,1)
View SolutionDetermine whether the f(x)=sinx function is strictly monotonic on the indicated interval.
(0,π)
View SolutionDetermine whether the f(x)=sinx function is strictly monotonic on the indicated interval.
(−π2,π2)
View SolutionFind the interval in which the function f(x)=sinx+cosx,0≤x≤2π is strictly increasing or strictly decreasing.
View Solution
