Determine whether the function is strictly monotonic on the indicated interval.
Solution in Malayalam
Step by step video & image solution for Determine whether the f(x)=sinx function is strictly monotonic on the indicated interval. (0,pi) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
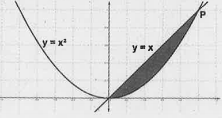
Consider the following figure
find the point of intersection (P) of the parabola and the line.
View SolutionFunction f(x)=(sinx)^(sinx) Interval [0, pi] Is defined as, then the function is
View SolutionVerify Rolle's theorem for each of the following functions on indicated intervals; f(x)=sin2x on 0≤x≤π f(x)=sinx+cosx−1 on [0,π2] f(x)=sinx−sin2x on [0,π]
View SolutionDetermine the intervals of monotonicity for the following functions :
f(x)=ln|x|,
View SolutionDetermine the intervals of monotonicity for the following functions :
f(x)=ex+5x
View SolutionDetermine whether the f(x)=x2 function is strictly monotonic on the indicated interval.
(−1,1)
View SolutionDetermine whether the f(x)=x2 function is strictly monotonic on the indicated interval.
(−1,0)
View SolutionDetermine whether the f(x)=x2 function is strictly monotonic on the indicated interval.
(0,1)
View SolutionDetermine whether the f(x)=x3−x function is strictly monotonic on the indicated interval.
(−1,0)
View SolutionDetermine whether the f(x)=x3−x function is strictly monotonic on the indicated interval.
(−1,−12)
View SolutionDetermine whether the f(x)=x3−x function is strictly monotonic on the indicated interval.
(−1,1)
View SolutionDetermine whether the f(x)=sinx function is strictly monotonic on the indicated interval.
(0,2π)
View SolutionDetermine whether the f(x)=sinx function is strictly monotonic on the indicated interval.
(−π2,π2)
View SolutionLet f(x)=sinx−cosx be defined on [0,2π]. Determine the intervals in which f(x) is strictly decreasing and strictly increasing.
View SolutionFind the intervals in which the function f given by f(x)=sinx+cosx, 0lexle2pi is strictly increasing or strictly decreasing.
View Solution
