Find the point on the curve y=x3−10x+8 at which the tangent is parallel to the line y=2x+1.Solution in Malayalam
Step by step video & image solution for Find the point on the curve y=x^3-10x+8 at which the tangent is parallel to the line y=2x+1. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
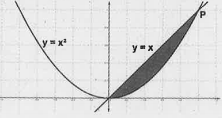
Consider the following figure
find the point of intersection (P) of the parabola and the line.
View SolutionFind the points on the curve x3−2x2−2x at which the tangent lines are parallel to the line y=2x−3 .
View SolutionFind a point on the curve y=3x2−2x−4 at which the tangent is parallel to the line 10x−y+7=0.
View Solutionवक्र x2+y2−2x−3=0 पर उन बिन्दुओ को ज्ञात कीजिए जिन पर स्पर्श रेखाएँ
X -अक्ष के समांतर है ,
View Solutionवक्र x2+y2−2x−3=0 पर उन बिन्दुओ को ज्ञात कीजिए जिन पर स्पर्श रेखाएँ
Y -अक्ष के समांतर है ।
View Solution(i) वक्र y=x2−x−8 पर ऐसा बिंदु कीजिए जिस पर स्पर्श रेखा X-अक्ष के समान्तर है |
(ii) वक्र y=x2−4x−32 पर ऐसा बिंदु ज्ञात कीजिए, जिस पर स्पर्श रेखा X-अक्ष के समान्तर है
(iii) वक्र y=2x2−6x−4 पर ऐसा बिंदु ज्ञात कीजिए जिस पर स्पर्श रेखा X-अक्ष के समान्तर है |
(iv) वृत्त x2+y2−2x−4y+1=0 के बिंदु पर स्पर्श रेखा X-अक्ष के समान्तर है ?
View SolutionFind the points on the curve x3−2x2−2x at which the tangent lines are parallel to the line y=2x−3 .
View SolutionFind the equation of tangent to the curve y=x3−2x2−2x at which tangent line is parallel to line y=2x−3.
View SolutionFind the point on the curve y=x3−10x+8 at which the tangent is parallel to the line y=2x+1.Is the given line tangent to the curve? Why?
View SolutionPoints at which the tangents to the hyperbola y=x−1x+1 are parllel to the line y=2x+1 are
View SolutionFind the equation of the tangent to the curve y=x2−2x+1 which is parallel to the line 2x−y+9=0.
View SolutionFind a point on the curve y=3x2−2x−4 at which the tangent is parallel to the line 10x−y+7=0.
View SolutionFind the points on the curve y=x3–3x2+2x at which the tangents to the curve is parallel to the line y-2x+3 = 0.
View SolutionFind the points on the curve y=x3−3x2+2x at which the tangent to the curve is parallel to the line y−2x+3=0.
View SolutionFind the points on the curve y=x3–3x2+2x at which the tangents to the curve is parallel to the line y-2x+3 = 0.
View Solution
