A curve passes through the origin, and its gradient function is 2x−x22.
Find the equation of the tangent at x=2.Solution in Malayalam
Step by step video & image solution for A curve passes through the origin, and its gradient function is 2x-x^2/2. Find the equation of the tangent at x=2. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
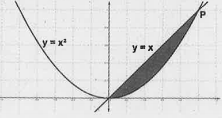
Consider the following figure
find the point of intersection (P) of the parabola and the line.
View SolutionThe equation of a curve passing through (2,72) and having gradient 1−1x2 at (x,y) is
View SolutionFind the equation of a curve, passes through (−2,3) at which the slope of tangent at any point (x,y) is 2xy2.
View SolutionFind the equation of the curve passing through origin and satisfying the differential equation 2xdy=(2x2+x)dx.
View SolutionThe gradient of the curve is given by dydx=2x−3x2.
The curve passes through (1, 2) find its equation.
View SolutionThe slope of the tangent at p(x,y) on the curve is −(y+3x+2). If the curve passes through the origin, find the equation of the curve.
View SolutionThe gradient (siope) of a curve at any point (x,y) is x2−4x2 . If the curve passes through the point (2 , 7) , then the equation of the curve is ,
View SolutionThe equation of a curve passing through (2,7/2) and having gradient 1−1x2at(x,y) is
View SolutionFind the equation of the curve passing through the point (2,−3), given that the slope of the tangent to the curve at any point (x,y) is 2xy2
View SolutionThe slope of the tangent at a point P(x,y) on a curve is (−y+3x+2). If the curve passes through the origin, find the equation of the curve.
View SolutionFind the equation of a curve passing through the point (2,3), given that the slope of the tangent to the curve at any point (x, y) is 2xy2.
View SolutionThe gradient at any point (x,y) of a curve is 3x2−12 and the curve through the point (2,-7).
Find the equation of the tangent at the point (2,-7).
View SolutionA curve passes through the origin, and its gradient function is 2x−x22.
Find its y coordinate when x=2.
View SolutionThe gradient of the curve is given by dydx=2x−3x2.
The curve passes through (1, 2) find its equation.
View SolutionFind the equation of the curve passing through origin and satisfying the differential equation 2xdy=(2x2+x)dx.
View Solution
