A rectangle sheet of tin with adjacent sides 45 cm and 24 cm is to be made into a box without top, by cutting off equal squares from the corners the folding up the flaps.
Taking the side of the square cut off as x, express the volume of the box as the function of x.Solution in Malayalam
Step by step video & image solution for A rectangle sheet of tin with adjacent sides 45 cm and 24 cm is to be made into a box without top, by cutting off equal squares from the corners the folding up the flaps. Taking the side of the square cut off as x, express the volume of the box as the function of x. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
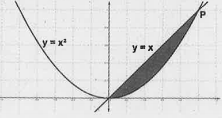
Consider the following figure
find the point of intersection (P) of the parabola and the line.
View SolutionA rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum ?
View SolutionA rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off squares from each corners and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum possible?
View SolutionA box of maximum volume with top open is to be made by cutting out four equal squares from four corners of a square tin sheet of side length a feet and then folding up the flaps. Find the side of the square cut-off.
View SolutionA rectangular sheet of tin 45 cm by 24 cm is to made into a box without top, by cutting-off square from each other corner and folding up the flaps. What should be the side of the square to be cut-off so that the volume of the box is maximum?
View SolutionA rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum ?
View SolutionA rectangular sheet of tin 45 cm by 24 cm is to made into a box without top, by cutting-off square from each other corner and folding up the flaps. What should be the side of the square to be cut-off so that the volume of the box is maximum?
View SolutionA rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum ?
View SolutionA rectangular sheet of tin 45 cm x 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is the maximum possible.
View SolutionA square ·piece of tin of side 12 cm is to be made into a box without a top by cutting a square from each corner and folding up the flaps to form a box. What should be the side of square to be cut off'. so that the volume of box is maximum and also find the volume of box.
View SolutionA rectangular sheet of tin 45 cm x 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is the maximum possible.
View SolutionA rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum ?
View SolutionAn rectangle sheet of tin with adjascent sides 45 cm and 24 cm is to be made into a box without top, by cutting off equal squares of side x from the corners the folding up the flaps.
For what value of x, the volume of the box will be maximum.
View SolutionA rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top by cutting off squares from the corners and folding up the flaps. What should be the side of the square in order the volume of the box is maximum.
View SolutionA box of maximum volume with top open is to be made by cutting out four equal squares from four corners of a square tin sheet of side length a feet and then folding up the flaps. Find the side of the square cut-off.
View Solution
