A planet is revolving about sun in an elliptical orbit. Choose the correct option based on the statements given below, (i) Areal velocity is constant. (ii) Arval velocity is proportional to velocity (iii) When planet is nearest to sun it's speed is maximum, (iv) Planet will move with constant speed. (v) Areal velocity is inversely proportional to velocity.
(i) is correct
(ii) is correct
(iv) is correct
(v) is correct
The correct Answer is:A
To solve the problem, we need to analyze each of the statements provided regarding a planet revolving around the Sun in an elliptical orbit. We will use Kepler's laws of planetary motion, particularly the second law, which relates to areal velocity.
1. Understanding Areal Velocity:
- Areal velocity is defined as the area swept out by the line connecting the planet to the Sun in a given time interval. According to Kepler's second law, this area is constant for equal time intervals.
- Conclusion: Statement (i) "Areal velocity is constant" is True.
2. Analyzing Areal Velocity and Velocity:
- Areal velocity is not directly proportional to the orbital velocity of the planet. While the planet's speed changes as it moves along its elliptical path, the areal velocity remains constant.
- Conclusion: Statement (ii) "Areal velocity is proportional to velocity" is False.
3. Speed of the Planet at Perihelion:
- The planet moves fastest when it is closest to the Sun (at perihelion) due to the gravitational pull being stronger and the conservation of angular momentum.
- Conclusion: Statement (iii) "When the planet is nearest to the Sun, its speed is maximum" is True.
4. Constant Speed of the Planet:
- The planet does not move with a constant speed; its speed varies as it travels along its elliptical orbit. It is fastest at perihelion and slowest at aphelion.
- Conclusion: Statement (iv) "Planet will move with constant speed" is False.
5. Areal Velocity and Velocity Relationship:
- Areal velocity is constant and does not change with the planet's velocity. Therefore, it cannot be inversely proportional to velocity.
- Conclusion: Statement (v) "Areal velocity is inversely proportional to velocity" is False.
Final Summary of Statements:
- (i) True
- (ii) False
- (iii) True
- (iv) False
- (v) False
Correct Options:
The correct options based on the analysis are statements (i) and (iii).
- Areal velocity is defined as the area swept out by the line connecting the planet to the Sun in a given time interval. According to Kepler's second law, this area is constant for equal time intervals.
- Conclusion: Statement (i) "Areal velocity is constant" is True.
- Areal velocity is not directly proportional to the orbital velocity of the planet. While the planet's speed changes as it moves along its elliptical path, the areal velocity remains constant.
- Conclusion: Statement (ii) "Areal velocity is proportional to velocity" is False.
- The planet moves fastest when it is closest to the Sun (at perihelion) due to the gravitational pull being stronger and the conservation of angular momentum.
- Conclusion: Statement (iii) "When the planet is nearest to the Sun, its speed is maximum" is True.
- The planet does not move with a constant speed; its speed varies as it travels along its elliptical orbit. It is fastest at perihelion and slowest at aphelion.
- Conclusion: Statement (iv) "Planet will move with constant speed" is False.
- Areal velocity is constant and does not change with the planet's velocity. Therefore, it cannot be inversely proportional to velocity.
- Conclusion: Statement (v) "Areal velocity is inversely proportional to velocity" is False.
- (i) True
- (ii) False
- (iii) True
- (iv) False
- (v) False
The correct options based on the analysis are statements (i) and (iii).
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
The angular momentum of a planet of mass M moving around the sun in an elliptical orbitis →L. The magnitude of the areal velocity of the planet is :
View SolutionA planet is revolving around the sun in an elliptical orbit. Which out of the following remains constant.
(a) Linear speed (b) angular momentum
( c) kinetic energy (d) potential energy (e) total energy throughout its orbit.
View Solution
Knowledge Check
For a planet revolving around Sun in an elliptical orbit, to obtain its velocity at any point we have to apply
AAngular momentum conservation about the sunBEnergy conservationCLinear momentum conservationDNewton's 2nd and 3nd law of motionA planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
A|v×r|B2|r×v|C∣∣∣12(r×v)∣∣∣DNone of theseA planet of mass m is revolving round the sun (of mass Ms) in an elliptical orbit. If →v is the velocity of the planet when its position vector from the sun is →r, then areal velocity of the positon vector of the planet is :
A→v+→rB→r×→vC12(→v×→r)D12(→r×→v)
A planet is revolving in an elliptical orbit around the sun as shown in the figure. The areal velocity (area swapped by the radius vector with respect to sun in unit time) is:
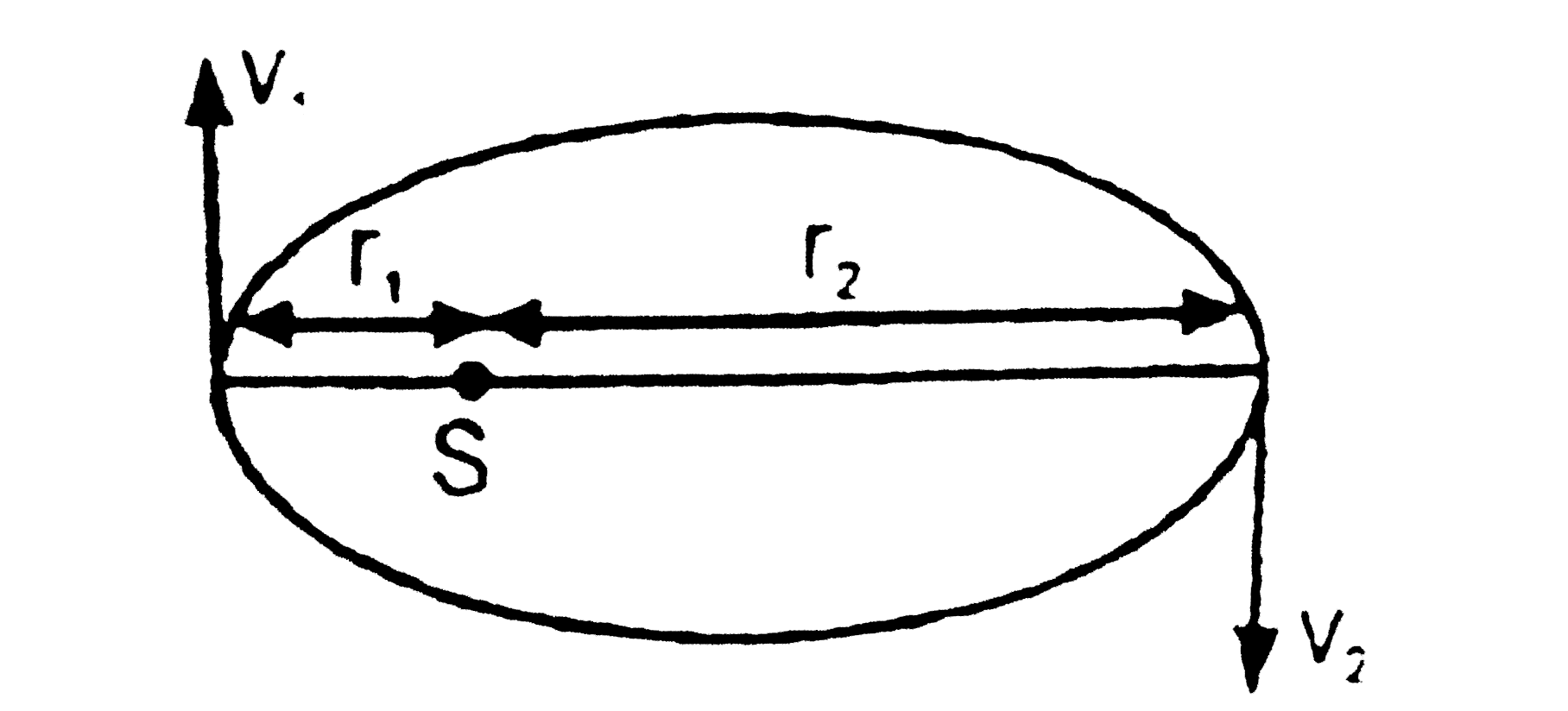
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the Sun is r and farthest distance is R. If the orbital velocity of the planet closest to the Sun is v, then what is the velocity at the farthest point?
View SolutionA planet is revolving around the sun in an elliptcal orbit. Its KE is different for different points and the total energy is negative. Its linear momentum is not conserved the eccentricity decides the shape of the orbit.
Velocity of the planet is minimum at
View SolutionA planet revolving in elliptical orbit has :
(A) a constant velocity of revolution.
(B) has the least velocity when it is nearest to the sun
(C) its areal velocity is directly proportional to its velocity
(D) areal velocity is inversely proportional to its velocity (E) to follow a trajectory such that the areal velocity is constant
Choose the correct answer from the options given below:
View SolutionA planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View Solution
