Question

A planet revolving in elliptical orbit has :
(A) a constant velocity of revolution.
(B) has the least velocity when it is nearest to the sun
(C) its areal velocity is directly proportional to its velocity
(D) areal velocity is inversely proportional to its velocity (E) to follow a trajectory such that the areal velocity is constant
Choose the correct answer from the options given below:

Options

A. A only
B. D only
C. C only
D. E only

Answer

D

Explanation

To solve the problem regarding a planet revolving in an elliptical orbit, we will analyze each statement based on Kepler's laws of planetary motion.

1. Understanding the Nature of Elliptical Orbits:
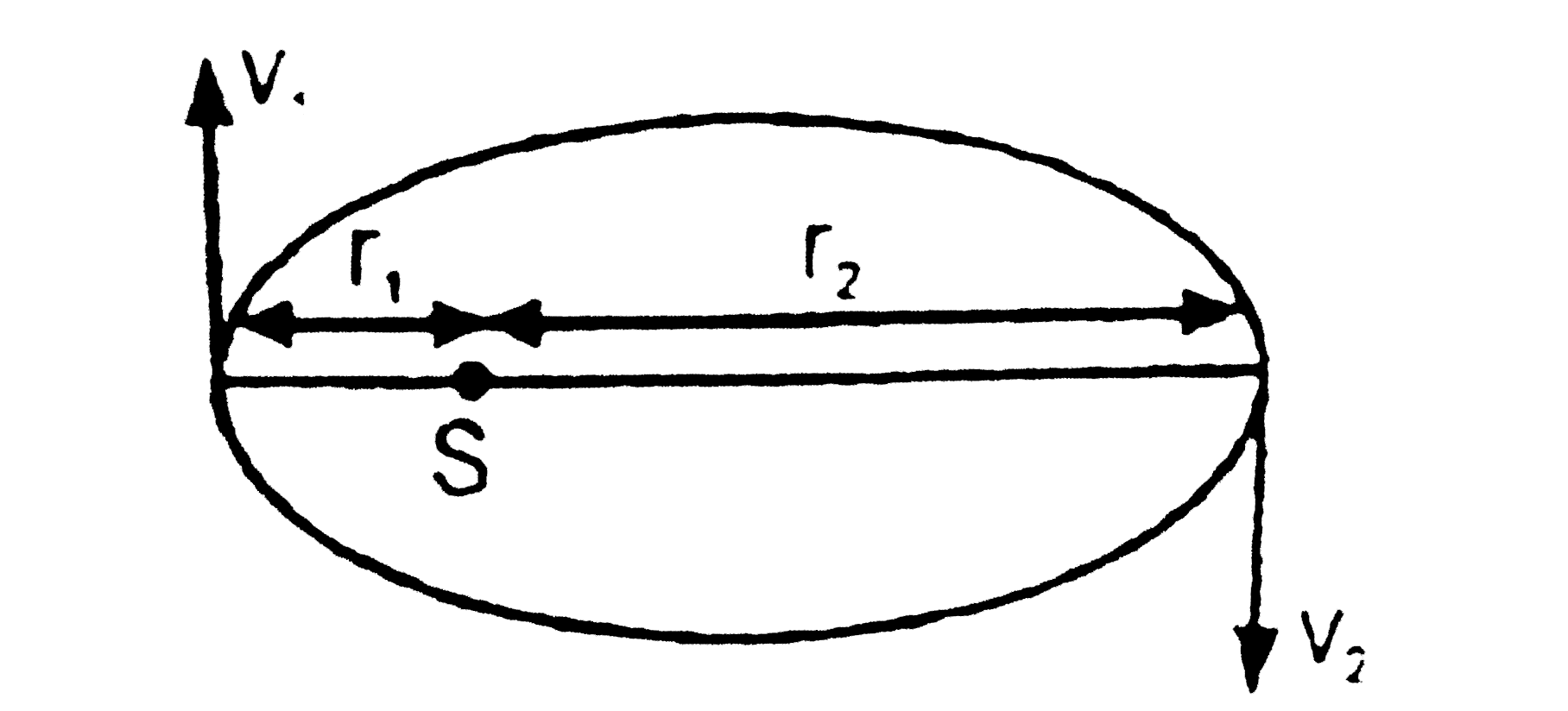
- According to Kepler's First Law, planets move in elliptical orbits with the Sun at one of the foci. This means the distance between the planet and the Sun changes as the planet moves along its orbit.

Hint: Recall that an ellipse has two foci, and in this case, the Sun occupies one of them.

2. Analyzing Statement A: "A planet revolving in elliptical orbits has a constant velocity of revolution."
- This statement is false. In an elliptical orbit, the speed of the planet varies; it moves faster when it is closer to the Sun (perihelion) and slower when it is farther away (aphelion).

Hint: Remember that the speed of a planet in an elliptical orbit is not constant due to the varying distance from the Sun.

3. Analyzing Statement B: "Has the least velocity when it is nearest to the Sun."
- This statement is also false. The planet has the highest velocity at perihelion (nearest to the Sun) and the lowest velocity at aphelion (farthest from the Sun).

Hint: Consider how gravitational forces and distance affect the speed of the planet.

4. Analyzing Statement C: "Its areal velocity is directly proportional to its velocity."
- This statement is false. Areal velocity (the area swept out per unit time) is constant for a planet in orbit, regardless of its instantaneous velocity. The areal velocity does not depend on the planet's speed.

Hint: Recall that Kepler's Second Law states that the line connecting a planet to the Sun sweeps out equal areas in equal times.

5. Analyzing Statement D: "Areal velocity is inversely proportional to its velocity."
- This statement is also false. Areal velocity remains constant, and it does not vary with the planet's velocity. Thus, it cannot be inversely proportional to it.

Hint: Think about how areal velocity is defined and how it relates to the orbit's geometry.

6. Analyzing Statement E: "To follow a trajectory such that the areal velocity is constant."
- This statement is true. According to Kepler's Second Law, a planet follows an elliptical trajectory that ensures its areal velocity remains constant.

Hint: Consider the implications of Kepler's laws on the motion of planets and how they relate to the area swept out over time.

Conclusion:
The correct answer is (E): "To follow a trajectory such that the areal velocity is constant."