यदि f(x)=[3x2+12x−1,−1≤x≤237−x ,2<x≤3 है , तब -
f(x),(−1,2) में वर्धमान होगा I
f(x),[−1,3] में संतत् है I
f'(2) विद्यमान नहीं है।
f(x) का अधिकतम मान x=2 पर है।
The correct Answer is:A, B, C, D
Step by step video, text & image solution for यदि f(x) = [{:(3x^2 + 12x -1",",-1 le x le 2),(37-x" ,",2 lt x le 3):} है , तब - by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - MONOTONOCITYEXERCISE - EXERCISE - 02 (सही विकल्पों को चुनिए (एक या एक से अधिक सही उत्तर हैं))16videos
MONOTONOCITY
- BOOK - ALLEN HINDICHAPTER - MONOTONOCITYEXERCISE - EXERCISE - 03 MISCELLANEOUS TYPE QUESTIONS ( स्तम्भ सुमेलन (Match the column) )1videos
MONOTONOCITY
- BOOK - ALLEN HINDICHAPTER - MONOTONOCITYEXERCISE - EXERCISE - 01 (सही विकल्प चुनिए (केवल एक सही उत्तर है))20videos
MONOTONOCITY
- BOOK - ALLEN HINDICHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - EXERCISE - 05 [B]12videos
METHODS OF DIFFERENTIATION
- BOOK - ALLEN HINDICHAPTER - PARABOLA EXERCISE - DO YOURSELF - 72videos
PARABOLA
Similar Questions
एक अवकलनीय फलन f(x),∀x∈R, एकदिष्ट वर्धमान है, तब -
12:05View Solutionनिम्न प्रश्न में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Column-II) के एक या एक से अधिक वक्तव्य (वक्तव्यों) से सही सुमेल करता है।
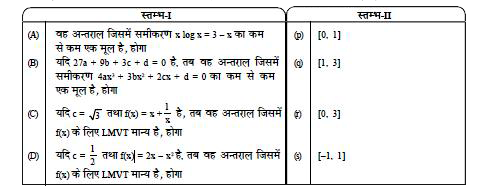 01:04View Solution
01:04View Solutionफलन f(x)=x2(x−2)2 है I
08:41View Solutionयदि ln (x+y) = 2xy हो , तो y'(0) =
02:24View Solutionरेखाओं x=4,y=4 तथा निर्देशी अक्षो से बने वर्गीय क्षेत्र को परवलय y2=4x तथा x2=4y विभाजित करते है। यदि S1,S2,S3 क्रमशः इन भागो के क्षेत्रफल ऊपर से नीचे की ओर अंकित है, तो S1:S2:S3 ज्ञात कीजिए।
08:45View SolutionIf f(x) = {{:( 3x ^(2) + 12 x - 1",", - 1 le x le 2), (37- x",", 2 lt x le 3):}, then
04:34View SolutionIf f(x)=⎧⎨⎩x220≤x<12x2−3x+321≤x≤2 then,
01:58View Solutionफलन f की अवकलनीयता की जाँच कीजिए
f(x)=⎧⎪⎨⎪⎩2x+3, यदि −3≤x<−2x+1,यदि −2≤x<0x+2,यदि 0≤x≤107:49View Solution∫31f(x)dxजहाँ f(x)={2x+1यदि 1≤x≤2x2+1यदि 2≤x≤3
02:36View SolutionIf f(x)={1+x0≤x≤23x−22<x≤3, then f(f(x)) is not differentiable at:
04:48View Solutionमूल्यांकित कीजिएः 4∫1f(x)dx, जहाँ f(x)={4x+3यदि 1≤x≤23x+5यदि 2≤x≤4
07:15View SolutionIf f(x)={x2+10≤x<1−3x+51≤x≤2
06:59View Solutionयदि f(x)=[3x2+12x−1,−1≤x≤237−x ,2<x≤3 है , तब -
01:58View Solutionf(x)={(x,0,≤,x,≤,2),(3x,−,1,2,<,x,≤,3) then f'(2+) is:
11:21View SolutionIf f(x)={3x2+12x−1−1≤x≤2 37−x2<x≤3, show that
f(x) is increasing in [-1, 2]03:04View Solution

