एक अवकलनीय फलन f(x),∀x∈R, एकदिष्ट वर्धमान है, तब -
f'(x)>∀x∈R
f'(x)≥0∀x∈R, जहाँ अवकलज कुछ परिमित बिन्दुओं पर शून्य हो जाता है।
f'(x)≥0∀x∈R जहाँ अवकलजकुछ विविक्त बिन्दुओं पर शून्य हो जाता है तथा इन विविक्त वन्दुओं की संख्या परिमित नहीं हा सकती है।
f'(x)≥0∀∈R जहाँ अवकलज अपरिमित विविक्त बिन्दुओं पर शून्य है।
The correct Answer is:C
Step by step video, text & image solution for एक अवकलनीय फलन f(x) , AA x in R, एकदिष्ट वर्धमान है, तब - by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MONOTONOCITYBOOK - ALLEN HINDICHAPTER - MONOTONOCITYEXERCISE - EXERCISE - 03 MISCELLANEOUS TYPE QUESTIONS ( स्तम्भ सुमेलन (Match the column) )
1 Videos
- MONOTONOCITYBOOK - ALLEN HINDICHAPTER - MONOTONOCITYEXERCISE - EXERCISE - 03 MISCELLANEOUS TYPE QUESTIONS कथन एवं कारण (Assertion & Reason)
3 Videos
- MONOTONOCITYBOOK - ALLEN HINDICHAPTER - MONOTONOCITYEXERCISE - EXERCISE - 01 (सही विकल्पों को चुनिए (एक या एक से अधिक सही उत्तर हैं))
5 Videos
- METHODS OF DIFFERENTIATIONBOOK - ALLEN HINDICHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - EXERCISE - 05 [B]
12 Videos
- PARABOLA BOOK - ALLEN HINDICHAPTER - PARABOLA EXERCISE - DO YOURSELF - 7
2 Videos
Similar Questions
निम्न प्रश्न में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Column-II) के एक या एक से अधिक वक्तव्य (वक्तव्यों) से सही सुमेल करता है।
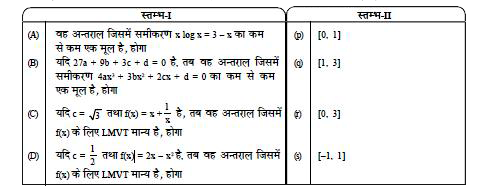
View Solutionनिम्न प्रश्नों में दो कथन दिए गए है, एक को कथन - I तथा दूसरे को कथन - II के रूप में अंकित किया गया है।
(A) कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण है।
(B) कथन- सत्य है, कथन-II सत्य है , कथन-II, कथन-I का सही स्पष्टीकरण नहीं है।
(C) कथन - I सत्य है परन्तु कथन - II असत्य है।
(D) कथन - I असत्य है परन्तु कथन - II सत्य है।
कथन-I: द्विघात समीकरण 10x2−28x+17=0 का कम से कम एक मूल [1,2] में होगा।
क्योंकि
कथन-II: f(x)=e10x(x−1)(x−2),[1,2] में रोल प्रमेय के सभी प्रतिबन्धों को सन्तुष्ट करता है।
View Solutionमाना h(x)=f(x)−(f(x))2+(f(x))3,∀x∈R हो, तो -
View Solutionयदि ln (x+y) = 2xy हो , तो y'(0) =
View Solutionरेखाओं x=4,y=4 तथा निर्देशी अक्षो से बने वर्गीय क्षेत्र को परवलय y2=4x तथा x2=4y विभाजित करते है। यदि S1,S2,S3 क्रमशः इन भागो के क्षेत्रफल ऊपर से नीचे की ओर अंकित है, तो S1:S2:S3 ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि फलन f(x)=|x|,x=0 पर अवकलनीय नहीं है यद्यपि यह x=0 पर संतत है|
View Solutionकोई फलन किसी बिन्दु x = a पर अवकलनीय कहलता है, जब -
View Solutionअन्तराल ज्ञात कीजिए जिन पर
f(x)=4sinx−2x−xcosx2+cosx
से प्रदत्त फलन f (i ) निरंतर वर्धमान (ii ) निरंतर ह्रासमान है।
View Solutionx के किन मानों के लिए फलन f(x)=x1+x2 वर्धमान तथा ह्रासमान है।
View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए गए अन्तराल में वर्धमान है ।
f(x)=logsinx,x∈(0,π2)
View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए गए अन्तराल में वर्धमान है ।
f(x)=x3−6x2+12x−1,x∈R
View Solutiona का न्यूनतम मान ज्ञात कीजिए कि फलन f(x)=x2+ax+5 अंतराल [1, 2] में वर्धमान है।
View Solutionवह अन्तराल ज्ञात कीजिए जिसमें फलन f(x) =x-[x] वर्धमान है।
View Solutionवह अन्तराल ज्ञात कीजिए जिसमें फलन f(x)=x−2x+1 एक वर्धमान फलन है।
View Solutionx के किन मानो के लिए फलन f(x)=(x)(x2+1 वर्धमान तथा हस्यमान है ?
View Solutionसिद्ध कीजिये कि (0,2π) में फलन f(x)=x−sinx वर्धमान है।
View Solution
