m द्रव्यमान के किसी कण के विस्थापन सदिश को इस प्रकार व्यक्त किया गया है - r(t)=ˆiAcosωt=ˆjBsinωt.
(a) दर्शाइए कि कण का गमन कोई दीर्घ वृत्त है।
(b) दर्शाइए कि F=−mω2r
Step by step video & image solution for m द्रव्यमान के किसी कण के विस्थापन सदिश को इस प्रकार व्यक्त किया गया है - r(t) = hat(i)A cos omega t = hat(j) B sin omega t. (a) दर्शाइए कि कण का गमन कोई दीर्घ वृत्त है। (b) दर्शाइए कि F = -m omega^(2) r by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- गति के नियम BOOK - NCERT EXEMPLAR HINDICHAPTER - गति के नियम EXERCISE - लघु उत्तरीय प्रश्न
8 Videos
- कार्य , ऊर्जा और शक्ति BOOK - NCERT EXEMPLAR HINDICHAPTER - कार्य , ऊर्जा और शक्ति EXERCISE - दीर्घ उत्तरीय प्रश्न
5 Videos
- गुरुत्वाकर्षणBOOK - NCERT EXEMPLAR HINDICHAPTER - गुरुत्वाकर्षणEXERCISE - दीर्घ उत्तरीय प्रश्न
4 Videos
Similar Questions
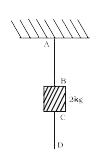
2kg का कोई द्रव्यमान किसी धागे AB द्वारा लटकाया गया है। इसी प्रकार का एक धागा CD 2kg द्रव्यमान के दूसरी ओर जोड़ा गया है। धागे AB को नीचे की ओर धीरे-धीरे बल बढ़ते हुए खींचा जाता है। कौन-सा धागा टूटेगा ? क्यों ?
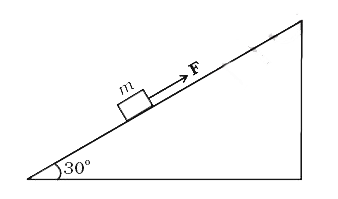
View Solutionक्षैतिज से 30∘ के कोण पर झके एक समतल पृष्ठ पर 1 kg द्रव्यमान का एक ब्लॉक इस आनत समतल के पृष्ठ के समांतर 10 N का बल लगाकर ऊपर की ओर धकेला जाता है। (चित्र )। ब्लॉक एवं आनत समतल के बीच घर्षण गुणांक 0.1 है। यदि ब्लॉक आनत समतल के अनुदिश 10 m की दूरी तक धकेला जाए तो, परिकलन कीजिए
(a) गुरुत्व के विरुद्ध किए गए कार्य की।
(b) घर्षण बल के विरुद्ध किए गए कार्य की ।
(c) स्थितिज ऊर्जा में हुई वृद्धि की।
(d) गतिज ऊर्जा में हुई वृद्धि की।
(e) लगाये गये बल द्वारा किये गये कार्य की।
View Solutionसूर्य के समान किसी तारे के चारो ओर कई पिंड विभिन्न दूरियों पर गति कर रहे है। यह मानिए कि सभी वृत्ताकार कक्षाओं में गमन करते है। मान लीजिये कि तारे के केंद्र से दुरी r है तथा इसका रैखिक वेग v, कोणीय वेग w, गतिज ऊर्जा K, गुरुत्वीय स्थैतिज ऊर्जा U, कुल ऊर्जा E तथा कोणीय संवेग L है । जैसे -जैसे कक्षा की त्रिज्या r में वृद्धि होती है, तो उपरोक्त राशियों में से किनमे वृद्धि होती है ओर किनमे कमी होती है ?
View SolutionIf vectors vec A=cos omega that i+sin omega that j and vec B=cos((omega t)/(2))hat i+sin((omega t)/(2))hat j are functions of time then the value of t at which they are orthogonal to each other is (A) t=(pi)/(w) (B) t=0( C) t=(pi)/(4w)( D) t=(pi)/(2w)
View SolutionConsider a particle moving in the x-y plane according to r=r (cos omegat hat(i)+sin omega t hat(j)) , where r and omega are constants. Find the trajectory, the velocity, and the acceleration.
View SolutionPosition vector of a particle moving in x−y plane at time t is r=a(1−cosωt)ˆi+asinωtˆj. The path of the particle is
View SolutionThe displacement vector of a particle of mass m is given by r (t) = hati A cos omega t + hatj B sin omega t . (a) Show that the trajectory is an ellipse. (b) Show that F = -m omega^(2)r .
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View Solutionकिसी कण का विस्थापन →r=A(ˆicosωt+ˆjsinωt) द्वारा व्यक्त किया जाता है। कण की गति है
View SolutionA body is acted upon by a force vec(F) , given by vec(F)=-k[(cos omega t)hat(i)+(sin omega t) hat(i)] undergoes displacement, where the position vector vec(r) of the body is given by vec(r)=a[cos ( omega t+ alpha) hat(i)+ sin ( omega t+ alpha) hat(j)] . Find the work done by the force from time t=0 to time t=2pi//omega .
View Solutionएक कण का स्थिति सदिश है।
r=(acosωˆi)+(asinωˆj)
इस कण का वेग होगा
View SolutionThe displacement vector of a particle of mass m is given by r (t) = ˆiAcosωt+ˆjBsinωt.
(a) Show that the trajectory is an ellipse.
(b) Show that F = −mω2r.
View SolutionIf Vectors →A=cosωtˆi+sinωtˆj and →B=(cos)ωt2ˆi+(sin)ωt2ˆjare functions of time. Then the value of t at which they are orthogonal to each other is
View SolutionPosition vector of a particle moving in x-y plane at time t is r=a(1- cos omega t)hat(i)+a sin omega t hat(j) . The path of the particle is
View SolutionA 0.2 kg mass particle bonding on a path: vec(r) = 2 cos omega t hat(i) + 3 sin omega t hat(j) Moves from Then the force on the particle is momentary with respect to the original point:
View Solution
