To remove the first degree terms in the following equations origin should be shifted to the another point then calculate the new origins from list - II
List - I List - II (A) x2−y2+2x+4y=0(1) (5,-7) (B) 4x2+9y2−8x+36y+4=0(2) (1,-2) (C) x2+3y2+2x+12y+1=0(3) (-1,2) (D) 2(x−5)2+3(y+7)2=10(4) (-1,-2) (5) (-5,7)
The correct matching is Solution in Telugu
ABCD4225
ABCD3241
ABCD5335
ABCD4331
The correct Answer is:D
Step by step video, text & image solution for To remove the first degree terms in the following equations origin should be shifted to the another point then calculate the new origins from list - II {:(" List - I "," List - II "),("(A) "x^(2)-y^(2)+2x+4y=0,"(1) (5,-7) "),("(B) "4x^(2) +9y^(2)-8x+36y + 4 = 0,"(2) (1,-2) "),("(C) "x^(2) + 3y^(2) + 2x + 12y + 1 = 0,"(3) (-1,2) "),("(D) "2(x-5)^(2)+3(y+7)^(2)=10,"(4) (-1,-2) "),(,"(5) (-5,7) "):} The correct matching is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHANGE OF AXESBOOK - AAKASH SERIESCHAPTER - CHANGE OF AXESEXERCISE - Additional Exercise
4 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MULTIPLE PRODUCT OF TWO VECTORS
21 Videos
- COMPOUND ANGLESBOOK - AAKASH SERIESCHAPTER - COMPOUND ANGLESEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) ADVANCED
5 Videos
Similar Questions
If the square ABCD where A(0,0), B(2,0), C(2,2), D(0,2) undergoes the following the transformations successively
(i) f1(x,y)→f(y,x)
(ii) f2(x,y)→f(x+3y,y)
(iii) f3(x,y)→f(x−y2,x+y2) then find nature of the final figure of ABCD
View SolutionIf →a,→b,→c are three coplanar vectors, ¯p,¯q,¯r are non-zero vectors then ∣∣ ∣ ∣∣¯p⋅¯a¯p⋅¯b¯p⋅¯c¯q⋅¯a¯q⋅¯b¯q⋅¯c¯r⋅¯a¯r⋅¯b¯r⋅¯c∣∣ ∣ ∣∣=
View SolutionIf sinx+cosx+tanx+cotx+secx+cosecx=7,0<x<π/2 and sin=2x=a−b√7 then (a,b∈Z+)
View SolutionWhen the origin is shifted to a suitable point, the equation 2x^(2)+y^(2)-4x+4y=0 transformed as 2x^(^^)2+y^^2-8x+8y+18=0^(@) The point to which origin was shifted is
View SolutionTo remvoe the first dgree terms in the equation 4x2+9y2−8x+36y+4=0, the origin in shifted to the point
View SolutionThe point to which the origin should be shifted in order to eliminate x and y terms in the equation 4x2+9y2−8x+36y+4=0 is
View SolutionThe point to which the origin should be shifted in order to eliminate x and y terms in the equation 4x2+9y2−8x+36y+4=0 is
View SolutionTo remove the first degree terms in the following equation origin should be shifted to the another point then calculate the new origins is
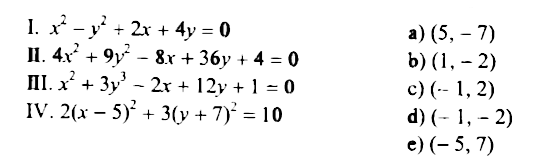
View SolutionThe point to which the origin is to be shifted to remove the first degree terms from the equation 2x2+4xy−6y2+2x+8y+1=0 is
View SolutionFind the point to which the origin has to be shifted to eliminate x and y terms in the equation 4x2+9y2−8x+36y+4=0
View SolutionFind the point to which the origin has to be shifted to eliminate x and y terms in the equation 4x2+9y2−8x+36y+4=0
View SolutionMatch the following from List-I to List-II
list−Ilist−IImajor axis of3(x−12)+4(y+22)=12y−√2=0minor axis of2(x+12)+3(y−12)=6x−2√2=0directirx ofx2+2y2=4y+2=0latus rectum of2x2+y2=4x+1=0
View SolutionIf origin is shifted to point (1,−2) then find the new transformed form of the following equation.
(i) 2x2+y2−4x+4y=0
(ii) y2−4x+4y+8=0
View SolutionThe point to which the origin should be shifted in order to eliminate x and y terms in the equation 4x2+9y2−8x+36y+4=0 is
View SolutionFind the point to which the origin has to be shifted to eliminate x and y terms in the equation 4x2+9y2−8x+36y+4=0
View Solution
