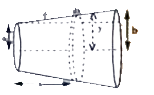
Figure shows a conductor of length l having a circular cross - section. The radius of cross - section varies linearly from a to b. The resistivity of the materia is ρ. Assuming that b−a<<l, find the resistance of the conductor.
tanϕ=b−a1=y−ax
yl−al=bx−ax
1(dydx)=(b−a)⇒dx=(1b−a)dy→(1)
Resistance across the elemental disc under consideration dR=ρdxA→(2)
from (1) and (2) dR=ρ(1b−a)dyπy2
⇒ Resistance across the given conductor,
R=∫by=adR⇒R=ρ1π(b−a).∫y=by=adyy2∴R=ρ1πab
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
101 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IB
44 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II PRACTICE SHEET (ADVANCED) (More than One correct answer Type Questions))
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
44 Videos
Similar Questions
Shown a conductor of length l having a circular cross section. The radius of cross section varies linearly form a→b. The resistivity of the material is(ρ).Assuming that b−a<<l,find the resistance of the conductor.

View SolutionShown a conductor of length l having a circular cross section. The radius of cross section varies linearly form a→b. The resistivity of the material is(ρ).Assuming that b−a<<l,find the resistance of the conductor.

View Solution
Knowledge Check
A conductor of length l and area of cross-section A has a resistance R then its specific resistance is
Aρ=RAlBρ=RAlCρ=lRADρ=R2AlResistivity of a conductor of length l and cross - section A is ρ . If its length is doubled and area of cross-section is halved, then its new resistivity will be .
Aρ2B4ρCρ4Dρ
Figure shows a conductor of length l having a circular cross-section. The radius of cross-section varies linearly from a to b. Find the resistance of the conductor. ltbtgt

View SolutionA conductor of length l has a non-uniform cross-section. The radius of cross-section varies linearly from a to b. The resistivity of the material is ρ. Find the resistance of the conductc across its ends.

View SolutionA conductor of length l has a non-uniform cross-section. The radius of cross-section varies linearly from a to b. The resistivity of the material is ρ. Find the resistance of the conductc across its ends.

View SolutionResistivity of a conductor of length l and cross - section A is ρ . If its length is doubled and area of cross-section is halved, then its new resistivity will be .
View SolutionResistance of a conductor of length l and area of cross-section A is R. If its length is doubled and area of cross-section is halved, then find its new resistance.
View SolutionResistance of a conductor of length l and area of cross-section A is R. If its length is doubled and area of cross-section is halved, then find its new resistance.
View Solution
