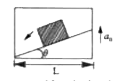
A block slides down from top of a smooth inclined plane of elevation θ fixed in an elevator going up with an acceleration a0. The base of incline has length L. Find the time taken by the block to reach the bottom.
Let us solve the problem in the elevator frame. The free body force diagram is shown. The forces are
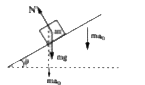
(i) N normal reaction to the plane,
(ii) mg acting vertically down,
(iii) ma0 (pseudo force). acting vertically down
If a is the acceleration of the body with respect to incline, taking components of forces
parallel to the incline.
mgsinθ+ma0sinθ=ma ∴ a=(g+a0)sinθ
This is the acceleration with respect to the elevator
The distance travelled is Lcosθ. If t is the time for reaching the bottom of icline.
Lcosθ=0+12(g+a0)sinθ.t2
t=[2L(g+a0)sinθcosθ]12=[4L(g+a0)sin2θ]12
Similar Questions
A block slides down from top of a smooth inclined plane of elevation ● fixed in an elevator going up with an acceleration a0 The base of incline hs length L Find the time taken by the block to reach the bottom
 .
.
View SolutionA block slides down from top of a smooth inclined plane of elevation ● fixed in an elevator going up with an acceleration a0 The base of incline hs length L Find the time taken by the block to reach the bottom
 .
.
View Solution
Knowledge Check
A particle slides down a smooth inclined plane of elevation , fixed in an elevator going up with an acceleration a0 (figure). The base of the incline has a length L. Find the time taken by the particle to reach to the bottom -
 A[2Lgsinθcosθ]1/2B[2L(g−a0)sinθcosθ]1/2C[2L(g+a0)cosθ]1/2D[2L(g+a0)sinθcosθ]1/2
A[2Lgsinθcosθ]1/2B[2L(g−a0)sinθcosθ]1/2C[2L(g+a0)cosθ]1/2D[2L(g+a0)sinθcosθ]1/2A particle slides down on a smooth incline of inclination 30∘, fixed in an elevator going up with an acceleration 2m/s2. The box of incline has width 4m. The time taken by the particle to reach the bottom will be
 A89√3sB98√3sC43√√32sD34√√32s
A89√3sB98√3sC43√√32sD34√√32s
A particle slides down a smooth inclined plane of elevation θ fixed in an elevator going up with an acceleration a0. The base of the incline has a length L. Find the time taken by the particle to reach the bottom.
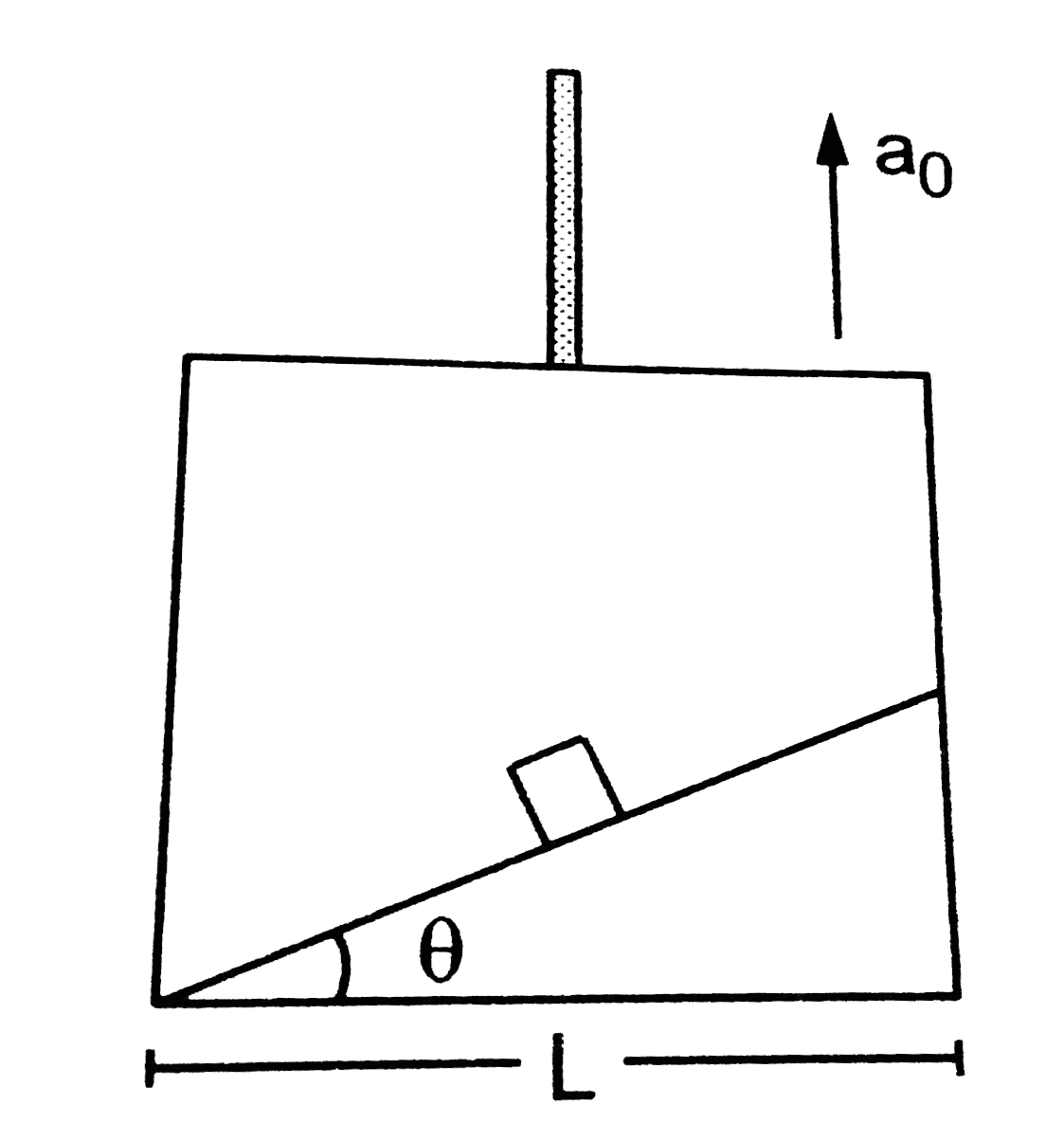
View SolutionA particle slides down a smooth inclined plane of elevation θ fixed in an elevator going up with an accelerationa0. The base of the incline has a length L.Find the time taken by the particle to reach the bottom.

View SolutionA particle slides down a smooth in clined plane of elevation θ fixed in an elevastor going up with an accelerationa0. The base of the incline has a length L.Find the time taken by the particle to reach the bottom.

View SolutionA particle slides down a smooth inclined plane of elevation θ fixed in a elevator going up with an acceleration a0. The base of the inline has a length L.
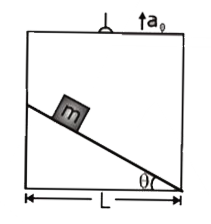
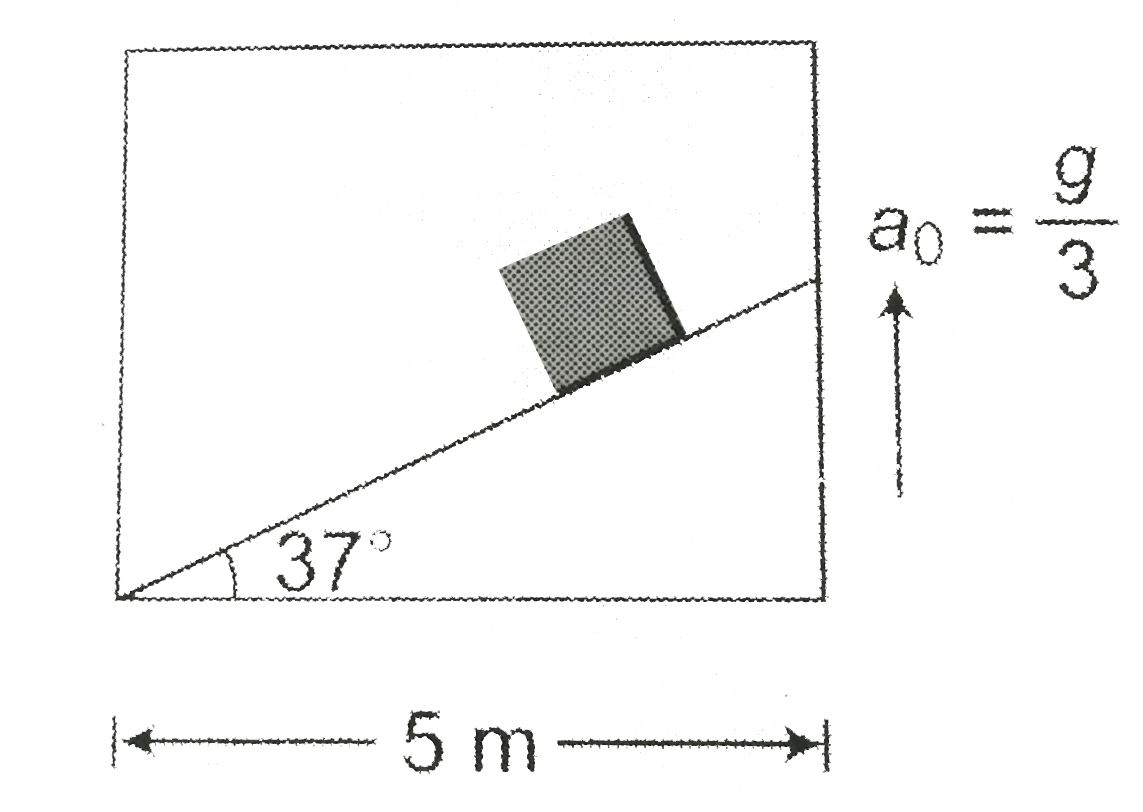
View SolutionA particle slides down a smooth incline of inclination 37∘, fixed in an elevator going up with an acceleration (g)/3. The base of incline has a length 5m. Find the time taken by the particle to reach the bottom.
View SolutionA particle slides down on a smooth incline of inclination 30∘, fixed in an elevator going up with an acceleration 2m/s2. The box of incline has width 4m. The time taken by the particle to reach the bottom will be

View Solution
