Two identical blocks A and B each of mass M are connected to each other through a ligh string. The system is placed on a smooth horizontal floor. When a constant force F is applied horizontally on the block A, find the tension in the string.
The acceleration of the system of two blocks A and
B=ForceTotal mass
∴a=FM+M=F2M
If we consider the free body diagram of A, the forces acting on it are (i) the applied force F and (ii) the tension T on the string as shown in the following fig.
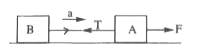
The resultant force =F−T,Ma=F−T
M(F2M)=F−T (∴a=F2M)
F2=F−T

T=F2 (or) From FBD for B
T=Ma=MF2M=F2
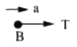
T=F2
Similar Questions
Two blocks of equal mass m are tied to each other through light string. One of the blocks is pulled along the line joining them with a constant force F. Find the tension in the string joining the blocks.
View SolutionTwo blocks o equal mass m are tied to each other through light string. One of the blocks is pulled along the line joining them with a constnt force F. Find the tension in the string joining the blocks.
View Solution
Knowledge Check
Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400NTwo blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400NFour blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.
 AT3=14FBT2=12FCT1=34FDT1=T2=T3=12F
AT3=14FBT2=12FCT1=34FDT1=T2=T3=12F
Two blocks A and B of masses m and M are attached with ideal string and pulley, and placed on smooth horizontal surface. Force F is applied horizontally as shown in figure. Find the ratio of the acceleration of A to that of B.

View SolutionTwo blocks A and B of masses m and M are attached with ideal string and pulley, and placed on smooth horizontal surface. Force F is applied horizontally as shown in figure. Find the ratio of the acceleration of A to that of B.

View SolutionTwo block of mass 1kg and 2kg are connected by a string AB of mass 1kg. The blocks are placed on a smooth horizontal surface. Block of mass 1kg is pulled by a horizontal force F of magnitude 8N. Find the tension in the string at points A and B

View SolutionThree identical cubes each of mass m are place on a smooth horizontal surface.A constant force F is applied on A as shown in the figure.The force on B applied by C is
View SolutionTwo blocks A and B each of 20 kg lying on a frictionless table are connected by a light string. The system is pulled horizontally with an acceleration of 2ms−2 by a force F on B. The tension in the string will be
View Solution
