A particle of mass m strikes a horizontal smooth floor with a velocity u making an angle 'θ' with the floor and rebound with velocity v making an angle 'ϕ' with the floor. The coefficient of restitution between the particle and the floor is e. Then
the impulse delivered by the floor to the body is mu(1+e) sin θ
tanϕ=etanθ
v=u√1−(1−e2)sin2θ
the ratio of the final kinetic energy to the initial kinetic energy is cos2θ=e2sin2θ
The correct Answer is:A, B, D
Similar Questions
A particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View SolutionA particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View Solution
Knowledge Check
A particle strikes a horizontal smooth floor with a velocity u making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. The coefficient of restitution between the particle and the floor is e.
AThe impulse delivered by the floor to the body is mu (1+e) sin θ.Btan ϕ=etanθ.Cv=u√1−(1−e2)sin2θDThe ratio of the final kinetic energy to the initial kinetic energy is cos2θ+e2sin2θ.A particle strikes a horizontal smooth floor with a velocity a making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. If the coefficient of restitution between the particle and the floor is e, then
Athe impulse delivered by the floor to the body is μ(1+e)sinθBtanϕ=etanθCv=u√1−(1−e)2sin2θDthe ratio of final kinetic energy to the initial kinetic energy is (cos2θ+e2sin2θ)A particle strikes a horizontal frictionless floor with a speed u, at an angle θ with the vertical, and rebounds with a speed υ, at an angle ϕ with the vertical. The coefficient of restitution between the particle and the floor is e. The angle ϕ is equal to :
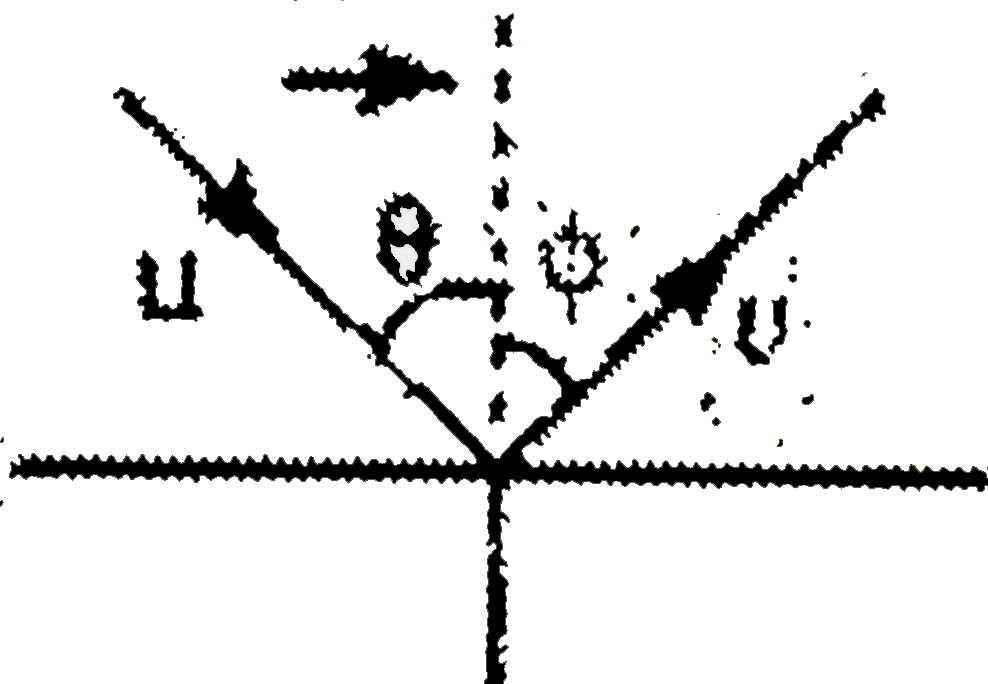 AθBtan−1[etanθ]Ctan−![1etanθ]D(1+e)θ
AθBtan−1[etanθ]Ctan−![1etanθ]D(1+e)θ
A particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The angle ϕ is equal to
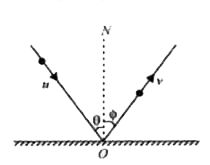
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle θ to the vertical, and rebounds with a speed v, at an angle ϕ to the vertical. The coefficient of restitution between the particle and the floor is e. The magnitude of v is
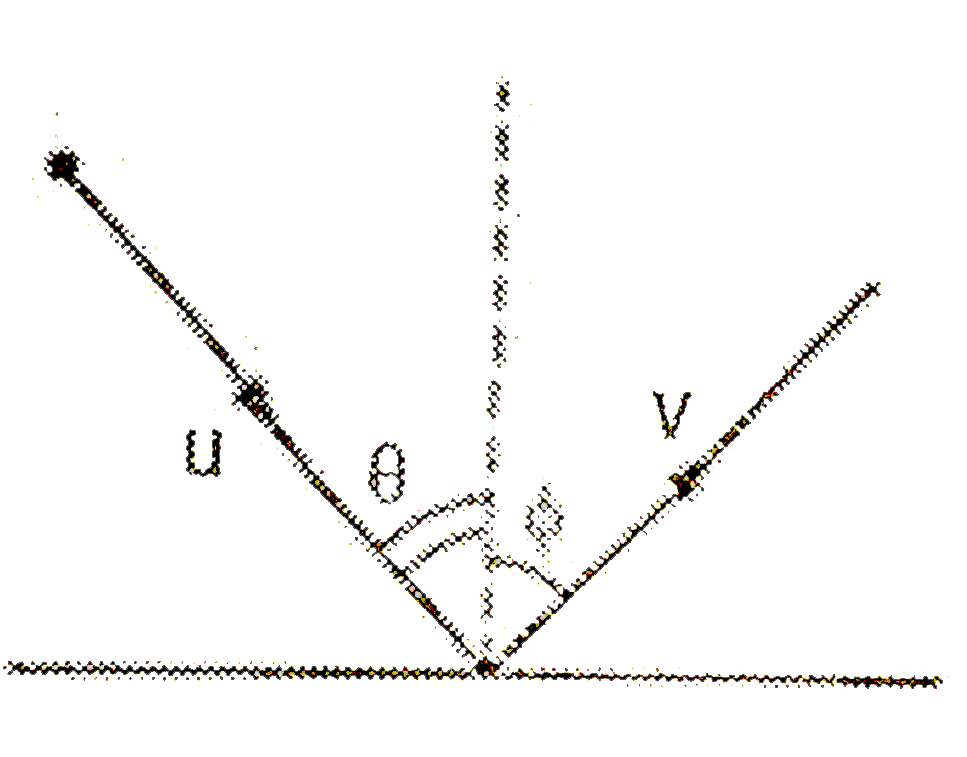
View SolutionA particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The magnitude of v is
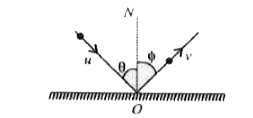
View SolutionA particle strikes a horizontal frictionless floor with a speed 'u' at an angle 'theta' with the vertical and rebounds with a speed 'v' at an angle 'alpha' with the vertical. Find the value of 'v' if 'e' is the coefficient of restitution.
View SolutionA ball is dropped from a height h onto a floor and rebounds to a height h/6. The coefficient of restitution between the ball and the floor is
View Solution
