The bob of a simple pendulum (mass m and length l ) dropped from a horizontal position strikes a block of the same mass elastically placed on a horizontal frictionless table. The K.E. of the block will be
2 mgl
mg//2
mgl
0
The correct Answer is:C
P.E. of bob at point A = mgl
This amount of energy will be converted into kinetic energy
∴ K.E. of bob at point B = mgl
and as the collision between bob and block (of same mass) is elastic so after collision bob will come to rest and total Kinetic energy will be transferred to block. So kinetic energy of block = mgl
Topper's Solved these Questions
- WORK , ENERGY , POWER AND COLLISIONBook:ERRORLESS Chapter:WORK , ENERGY , POWER AND COLLISIONExercise:Ordinary Thinking (Objective Questions) (Power)
Explore 31 Videos
- WORK , ENERGY , POWER AND COLLISIONBook:ERRORLESS Chapter:WORK , ENERGY , POWER AND COLLISIONExercise:Ordinary Thinking (Objective Questions) (Elastic and Inelastic Collision)
Explore 68 Videos
- WORK , ENERGY , POWER AND COLLISIONBook:ERRORLESS Chapter:WORK , ENERGY , POWER AND COLLISIONExercise:Ordinary Thinking (Objective Questions) (Work Done by Variable Force)
Explore 26 Videos
- WAVES AND SOUNDBook:ERRORLESS Chapter:WAVES AND SOUNDExercise:SET
Explore 25 Videos
- WORK, ENERGY, POWER & COLLISIONBook:ERRORLESS Chapter:WORK, ENERGY, POWER & COLLISIONExercise:Assertion
Explore 30 Videos
Similar Questions
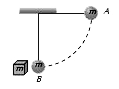
The bob of a simple pendulum of length l dropped from a horizontal position strikes a block of the same mass, placed on a horizontal table (frictionless) as shown in the diagram, the block shall have kinetic energy-

View SolutionIf a simple pendulum of mass m is released from a horizontal position, find the tension in the string as a function of the angle θ with the horizontal.
View Solution
Knowledge Check
A simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
AmL√2gLBmL√gLCmL√3gLDnoneThe bob of a simple pendulum of length L, is displaced through 90∘, from its mean position and then released. What will be the tension in the string when the bob of mass m will be its lowest position ?
AmgB2 mgC3 mgD6 mgThe bob of a simple pendulum of length L, is displaced through 90∘, from its mean position and then released. What will be the tension in the string when the bob of mass m will be at its lowest position?
AmgB3 mgC2 mgD6 mg
A horizontal force of 4 N is applied to a block of mass 2 kg resting on a frictionless table. What is the acceleration of the block in ms−2 ?
View SolutionA simple pendulum , made of a string of length l and a bob of mass m, is released from a small angle θ0 it strikes a block of mass M, kept on a horizontal surface at its lowest point of oscil,ations , elastically , it bounces back and goes up to an angle θ)(1−) then M is given by :
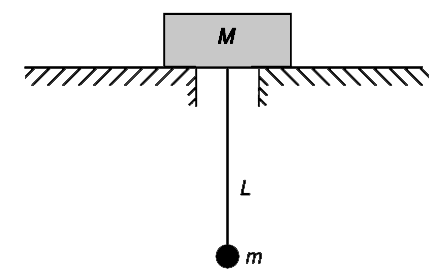
View SolutionA block of mass M rests on a smooth horizontal table. There is a small gap in the table under the block through which a pendulum has been attached to the block. The bob of the simple pendulum has mass m and length of the pendulum is L. The pendulum is set into small oscillations in the vertical plane of the figure. Calculate its time period. The table does not interfere with the motion of the string.
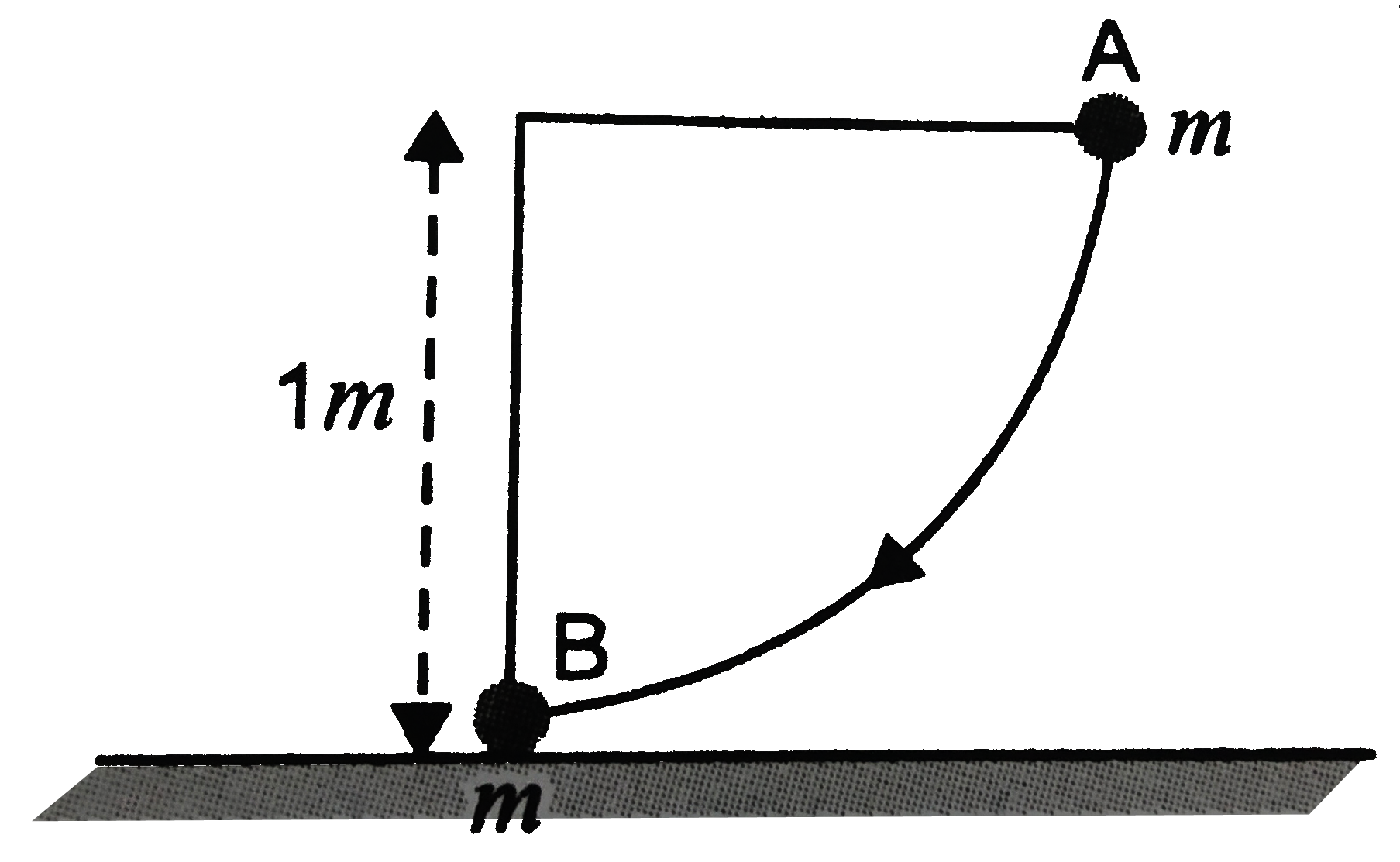
View SolutionThe bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.
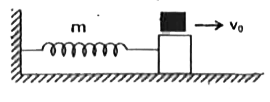
View SolutionA spring of mass m lies on a smooth table. One, end of it is clamped to the vertical wall and other end is attached to a mass m ( as shown in fig) and is placed on a horizontal frictionless surface. If the block of mass M is given a velocity v0 towards right find the K.E. of the system . ( AsSigmae velocity in spring is varying linearly).
View Solution