Question

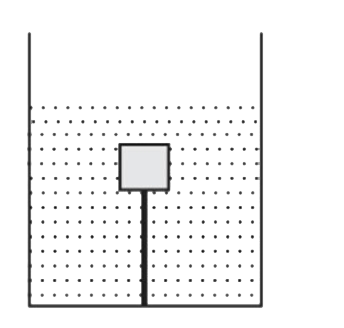
A small wooden block of density $400kg/m^3$ is released from rest inside a swimming pool filled with water of density ${10}^{3}kg/m^3$. The acceleration of the block just after it is released is __________ $m/s^2(g=10m/s^2)$

Answer

15

Explanation

To find the acceleration of the wooden block just after it is released in water, we can follow these steps:

Step 1: Identify the Given Data
- Density of the wooden block, \( \rho_b = 400 \, \text{kg/m}^3 \)
- Density of water, \( \rho_w = 1000 \, \text{kg/m}^3 \)
- Acceleration due to gravity, \( g = 10 \, \text{m/s}^2 \)

Step 2: Determine the Forces Acting on the Block
When the block is submerged in water, two main forces act on it:
1. The weight of the block (\( W \)) acting downwards:
\( W = mg = \rho_b V g \)
where \( V \) is the volume of the block.

2. The buoyant force (\( F_b \)) acting upwards, which is equal to the weight of the water displaced by the block:
\( F_b = \rho_w V g \)

Step 3: Calculate the Net Force Acting on the Block
The net force (\( F_{net} \)) acting on the block can be calculated as:
\( F_{net} = F_b - W \)
Substituting the expressions for \( F_b \) and \( W \):
\( F_{net} = \rho_w V g - \rho_b V g \)
Factoring out \( Vg \):
\( F_{net} = Vg (\rho_w - \rho_b) \)

Step 4: Apply Newton's Second Law
According to Newton's second law, the net force is also equal to the mass of the block times its acceleration (\( a \)):
\( F_{net} = ma \)
The mass of the block (\( m \)) is given by:
\( m = \rho_b V \)
Thus, we can write:
\( Vg (\rho_w - \rho_b) = \rho_b V a \)

Step 5: Simplify the Equation
Dividing both sides by \( V \) (assuming \( V \neq 0 \)):
\( g (\rho_w - \rho_b) = \rho_b a \)
Now, solving for \( a \):
\( a = \frac{g (\rho_w - \rho_b)}{\rho_b} \)

Step 6: Substitute the Values
Substituting the known values:
\( a = \frac{10 \, \text{m/s}^2 \times (1000 \, \text{kg/m}^3 - 400 \, \text{kg/m}^3)}{400 \, \text{kg/m}^3} \)
\( a = \frac{10 \, \text{m/s}^2 \times 600 \, \text{kg/m}^3}{400 \, \text{kg/m}^3} \)
\( a = \frac{6000 \, \text{m/s}^2}{400} \)
\( a = 15 \, \text{m/s}^2 \)

Final Answer
The acceleration of the block just after it is released is \( 15 \, \text{m/s}^2 \).

---