A cubical block of wood, of length 10 cm, floats at the interface between oil of density $800 k g / m^{3}$ and water. The lower surface of the block is 1.5 cm below the interface. If the depth of water is 10 cm below the interface and oil is upto 10 cm above the interface then the difference in pressure at the lower and the upper face of the wooden block is (Assume density of water $ρ = 1000 k g / m^{3}$ ) and acceleration of gravity , $g = 10 m / s^{2}$ )

A

850 Pa

B

780 Pa

C

800 Pa

D

830 Pa

Text Solution

Verified by Experts

The correct Answer is:D

Given, length of cubical block, l = 10 cm = 0.1 m
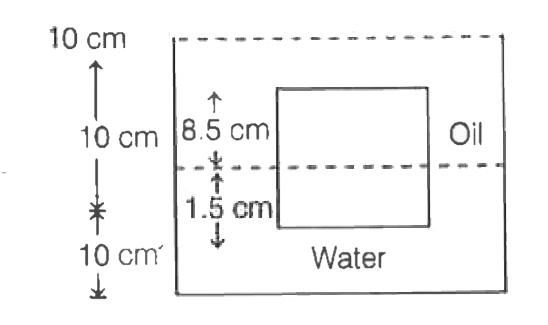density of oil $ρ_{0} = 800 k g / m^{3}$
and density of water, $ρ_{w} = 10^{3} k g / m^{3}$
If $V_{1}$ and $V_{2}$ be the volume of wooden block in water and oil respectively, then
$V_{1} : V_{2} = 1.5 : 8.5$
$\frac{V_{1}}{V_{2}} = \frac{1.5}{8.5} = 3.17$
$∴ V_{1} = \frac{3}{17} V_{2} ... (i)$
$∴ V_{1} + V_{2} = V$ where is the volume of the block From Eq. (1), we get
$\frac{3}{17} V_{2} + V_{2} = V \Rightarrow V_{2} = \frac{17}{20} V$
$∴ V_{1} = \frac{3}{20} V$
If $ρ$ be the density of the block weight of block
$∴$ weight of oil displaced + weight of water displaced
$V ρ G = V_{1} ρ_{ω} g + V_{2} ρ_{o i l} g$
$V ρ g = \frac{3}{20} V ρ_{w} g + \frac{17}{20} V ρ_{o i l} g$
$ρ = \frac{3}{20} ρ_{w} + \frac{17}{20} ρ_{o i l} = \frac{3}{20} \times 10000 + \frac{17}{20} \times 800$
$= 830 k g / m^{3}$
$∴$ Pressure difference
$p = ρ g h = 830 \times 10 \times 0.1 = 830 P a$

Updated on:21/07/2023

|

Class 12 PHYSICS TS EAMCET 2019 (4 MAY SHIFT 2)

Topper's Solved these Questions

Similar Questions

Knowledge Check

A cubical block of wood 10 cm on a side floats at the interface between oil and water with its lower surface horizontal and 4 cm below the interface. The density of oil is $0.6 g c m^{- 3}$ . The mass of block is

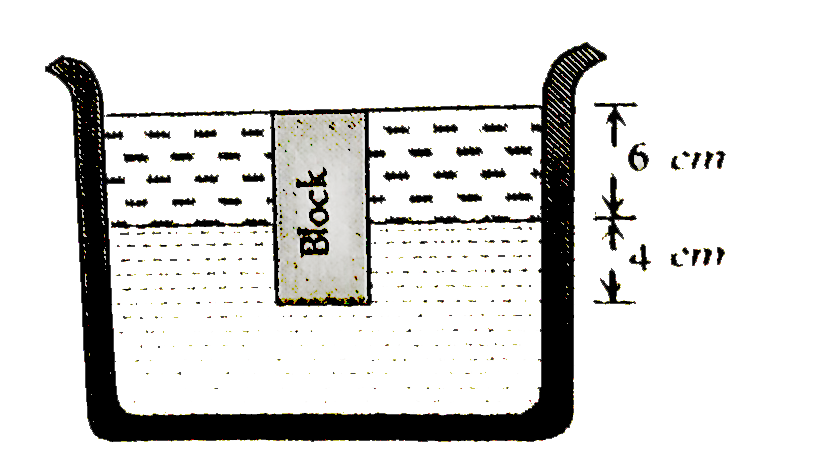A $706 g$
B $607 g$
C $760 g$
D $760 g$
A cubical block of side 10 cm floats at the interface of an oil and water. The pressure above that of atmosphere at the lower face of the block is

A $200 N m^{- 2}$
B $680 N m^{- 2}$
C $400 N m^{- 2}$
D $800 N m^{- 2}$
A cubical block of wood $10 c m$ on a side floats at the interface between oil and water, as in fig. with its lower face $2 c m$ below the interface. The intensity of the oli is $0.6 g c m^{- 3}$ . The mass of the block is $1 k g$

A340g
B680g
C80g
D10g

TS EAMCET PREVIOUS YEAR PAPERS-TS EAMCET 2019 (4 MAY SHIFT 2)-PHYSICS

Home
Ask Doubt
Profile