P is a variable point on the curve y= f(x) and A is a fixed point in the plane not lying on the curve. If PA2 is minimum, then the angle between PA and the tangent at P is
Step by step video & image solution for P is a variable point on the curve y= f(x) and A is a fixed point in the plane not lying on the curve. If PA^(2) is minimum, then the angle between PA and the tangent at P is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Tangents are drawn from the point (4, 2) to the curve x2+9y2=9, the tangent of angle between the tangents :
A3√35√17B√4310C√435D√317Let a curve P:(y−2)2=x−1 If a tangent is drawn to the curve P at the point whose ordinate is 3 then the area between the tangent , curve and x-asis is
A9B11C92D112The minimum distance between a point on the curve y=ex and a point on the curve y=logex is -
A1√2B√2C√3D2√2
The minimum distance between a point on the curve y=ex and a point on the curve y=logex is
View SolutionA curve y=f(x) passes through the point P(1,1). The normal to the curve at P is a(y−1)+(x−1)=0. If the slope of the tangent at any point on the curve is proportional to the ordinate of the point. Determine the equation of the curve. Also obtain the area bounded by the y-axis, the curve and the normal to the curve at P.
View SolutionTangents PA and PB are drawn to the circle x2+y2=4 from an external point P lying on the Time y = x such that the angle θ between the tangents satisfies π3≤θ≤2π3. The co - ordinates of the point P, if the perimeter of ΔPAB is maximum for all θ are
View Solution2 equal tangents PA and PB are drawn from an external point P on a circle with centre O. What is the length of each tangent, if P Is 12 cm from the centre and the angle between the tangents is 120∘ ?
View SolutionLet f(x)=⎡⎢ ⎢⎣1−x0≤x≤101<x≤2andg(x)=∫x0f(t)dt.(2−x)22<x≤3
Let the tangent to the curve y=g(x) at point P whose abscissa is 52 cuts x-axis in point Q.
Let the pependiculat from point Q on x-axis meets the curve y=g(x) in point R.
If 'θ' be the angle between tangents to the curve y=g(x) at point P and R, then tanθ equals to :
View Solution
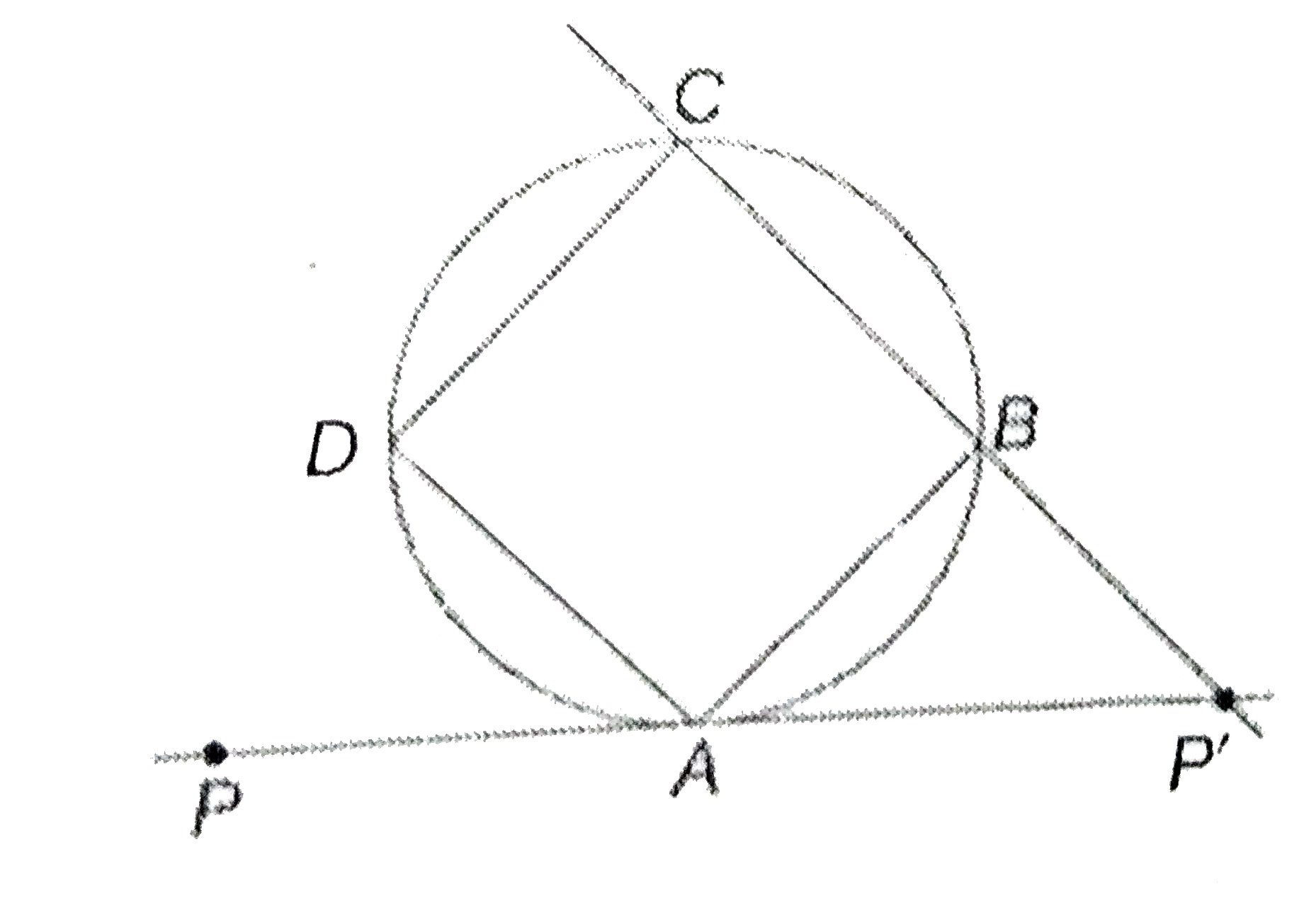 If ABCD is a square incribed in a circle and PA is a tangent, then the angle between the lines P'A and P'B is _________.
If ABCD is a square incribed in a circle and PA is a tangent, then the angle between the lines P'A and P'B is _________.