2 equal tangents PA and PB are drawn from an external point P on a circle with centre O. What is the length of each tangent, if P Is 12 cm from the centre and the angle between the tangents is 120∘ ?
24 cm.
6 cm.
8 cm.
Cannot be determined
The correct Answer is:B
To solve the problem, we need to find the length of the tangents PA and PB drawn from an external point P to a circle with center O. Given that the distance from P to O is 12 cm and the angle between the tangents PA and PB is 120 degrees, we can follow these steps:
1. Understand the Geometry:
- We have a circle with center O.
- Point P is outside the circle, and two tangents PA and PB are drawn from point P to points A and B on the circle.
- The angle ∠APB is given as 120 degrees.
2. Bisect the Angle:
- The line segment OP bisects the angle ∠APB.
- Therefore, ∠APO = ∠BPO = 60 degrees (since 120 degrees divided by 2 equals 60 degrees).
3. Identify Right Triangles:
- The segments OA and OB are perpendicular to the tangents PA and PB at points A and B, respectively.
- This means we can analyze the right triangle OAP (or OBP).
4. Apply Trigonometry:
- In triangle OAP, we know:
- OP (hypotenuse) = 12 cm
- ∠APO = 60 degrees
- We need to find the length of the tangent PA.
- Using the cosine function:
cos(60∘)=PAOP
- We know that cos(60∘)=12.
5. Set Up the Equation:
- Substitute the known values into the equation:
12=PA12
6. Solve for PA:
- Rearranging gives:
PA=12×12=6 cm
7. Conclusion:
- Since PA and PB are equal (both are tangents from the same external point), we conclude:
PB=PA=6 cm
Final Answer:
The length of each tangent PA and PB is 6 cm.
---
- We have a circle with center O.
- Point P is outside the circle, and two tangents PA and PB are drawn from point P to points A and B on the circle.
- The angle ∠APB is given as 120 degrees.
- The line segment OP bisects the angle ∠APB.
- Therefore, ∠APO = ∠BPO = 60 degrees (since 120 degrees divided by 2 equals 60 degrees).
- The segments OA and OB are perpendicular to the tangents PA and PB at points A and B, respectively.
- This means we can analyze the right triangle OAP (or OBP).
- In triangle OAP, we know:
- OP (hypotenuse) = 12 cm
- ∠APO = 60 degrees
- We need to find the length of the tangent PA.
- Using the cosine function:
cos(60∘)=PAOP
- We know that cos(60∘)=12.
- Substitute the known values into the equation:
12=PA12
- Rearranging gives:
PA=12×12=6 cm
- Since PA and PB are equal (both are tangents from the same external point), we conclude:
PB=PA=6 cm
The length of each tangent PA and PB is 6 cm.
Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
90 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF
25 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
90 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
PA and PB are two tangents drawn from an external point P to a circle with centre C and radius=4cm If PA⊥PB then length of each tangent is
View SolutionTwo tangents AB and AC are drawn from an external point A to a circle with centre O . If they are inclined to each other at an angle of 100∘ then what is the value of ∠BOC.
View Solution
Knowledge Check
The pair of tangents AP and AQ drawn from an external point to a circle with centre O are perpendicular to each other. If the length of each tangent is 5 cm , then radius of the circle is
A10 cmB7.5 cmC5 cmD2.5 cmIf tangent PA and PB from a point P to a circle with centre O are inclined to each other at angle 80∘, then ∠POA is equal to
A50∘B60∘C70∘D80∘
The lengths of tangents drawn from an external point to a circle are ________.
View SolutionIn figure ,PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm .If Pa⊥PB ,then the length of each tangent is :

View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 110∘ , find ∠POA.
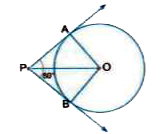
View SolutionIn Fig . pair of tangents AP and AQ drawn from an external point A to a circle with centre O are perpendicular to each other and length of each tangent is 5 cm. Find the radius of the circle.
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80∘, then ∠POA is equal to
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80∘ , then find ∠POA .
View Solution