तीन सर्वसम बल्य B1,B2 तथा B3 में दर्शाए अनुसार संयोजित हैं। जब तीनों बल्व चमकते हैं, तो ऐमीटर A का पाद्शक 3A होता है।
(i) यदि बल्ब B1 फ्यूज हो जाए, तो अन्य दो बल्चों को चमक पर क्या प्रभाव पड़ेगा?
(ii) यदि वल्च B2 पशूज हो जाए तो A1.A2...A3 तथा A के पाठ्यांकों पर क्या प्रभाण पड़े?
(iii) जब तीनों बल्ब एक साथ चमकते परिपथ में कितनी शक्ति क्षय होती है?
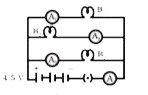
(i) B2 तथा B3 बल्ब की चमक समान रहेगी। (ii) A1 1 ऐम्पियर दर्शएगा, A2 शून्य दर्शाएगा. A3 1 ऐम्पियर द्शएगा तथा A का पाठ्याक 2 ऐम्पियर होगा
(iii) P=V×I=4.5V×3A−13.5W
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR HINDICHAPTER - विद्युतEXERCISE - दीर्घउत्तरीय प्रश्न7videos
विद्युत
- BOOK - NCERT EXEMPLAR HINDICHAPTER - मानव नेत्र तथा रंगबिरंगा संसारEXERCISE - दीर्घ उत्तरीय प्रश्न6videos
मानव नेत्र तथा रंगबिरंगा संसार
- BOOK - NCERT EXEMPLAR HINDICHAPTER - विद्युत धारा के चुंबकीय प्रभावEXERCISE - दीर्घउत्तरीय प्रश्न8videos
विद्युत धारा के चुंबकीय प्रभाव
Similar Questions
तीन तापदीप्त लैप, जिनमें प्रत्येक 100W: 220V का है, किसी 220V आपूर्ति के विद्युत परिपक्ष में श्रेणीक्रम में संयोजित हैं। किसी अना परिपत्र में समान विद्युत स्नान से यहीं तोनों
(a) क्या दोनों परिपथों में बल्य समान तीव्रता में चमकेंगे? अपने उत्तर की पुष्टि कीजिए। लैप पार्यक्रम में संयोजित हैं।
(b) अब, मान लीजिए दोनों परिपथों का एक-एक बल्ब प्यूज हो जाता है. तो क्या प्रत्येक परिपथ में बाकी बच बल्ब लगातार चमकते रहेंगे। कारण लिखिए।02:15View Solutionमानव नेत्र की संरचना तथा कार्यविधि स्पष्ट कीजिए | हम पास को देखने योग्य कैसे बन जाते हैं ? दूर दोनों की वस्तुओं को देखने योग्य कैसे बन जाते है ?
04:01View Solutionउत्तर दक्षिण की ओर संकेत करने वाली चुंबकीय दिक्सूची, जिसके समीप कोई चुंबक नहीं है, के निकट कोई छड़ चुंबक अथवा धारावाही पाश लाने पर, विक्षेपित क्यों हो जाती है? चुंबकीय क्षेत्र रेखाओं की परिकल्पना के कुछ प्रमुख लक्षणों का वर्णन कीजिए।
05:35View Solutiondet[[2a_(1)b_(1),a_(1)b_(2)+a_(2)b_(1),a_(1)b_(3)+a_(3)b_(1)a_(1)b_(2)+a_(2)b_(1),2a_(2)b_(2),a_(2)b_(3)+a_(3)b_(2)a_(1)b_(3)+a_(3)b_(1),a_(3)b_(2)+a_(2)b_(3),2a_(3)b_(3)]]=
05:10View SolutionSuppose a1,a2,a3 are in A.P. and b1,b2,b3 are in H.P. and let △=∣∣ ∣∣a1−b1a1−b2a1−b3a2−b1a2−b2a2−b3a3−b1a3−b2a3−b3∣∣ ∣∣
then01:59View SolutionThe value of the determinant
Δ=∣∣ ∣ ∣ ∣ ∣ ∣∣1−a31b311−a1b11−a31b321−a1b21−a31b331−a1b31−a32b311−a2b11−a32b321−a2b21−a32b331−a2b31−a33b311−a3b11−a33b321−a3b21−a33b331−a3b3∣∣ ∣ ∣ ∣ ∣ ∣∣, is05:25View SolutionSuppose four distinct positive numbers a1,a2,a3,a4 are in G.P. Let b1=a1+,ab=b1+a2,b3=b2+a3andb4=b3+a4.
Statement -1 : The numbers b1,b2,b3,b4 are neither in A.P. nor in G.P.
Statement -2: The numbers b1,b2,b3,b4 are in H.P.02:50View Solutionthe value of the determinant
∣∣ ∣ ∣ ∣ ∣∣(a1−b1)2(a1−b2)2(a1−b3)2(a1−b4)2(a2−b1)2(a2−b2)2(a2−b3)2(a3−b4)2(a3−b1)2(a3−b2)2(a3−b3)2(a3−b4)2(a4−b1)2(a4−b2)2(a4−b3)2(a4−b4)2∣∣ ∣ ∣ ∣ ∣∣ is02:14View SolutionLet = ∣∣ ∣∣2a1b1a1b2+a2b1a1b3+a3b1a1b2+a2b12a2b2a2b3+a3b2a1b3+a3b1a3b2+a2b32a3b3∣∣ ∣∣
Express the determinant D as a product of two determinants. Hence or otherwise show that D = 0.02:00View SolutionSuppose a1,a2,a3 are in A.P. and b1,b2,b3 are in H.P. and let Δ=∣∣ ∣∣a1−b1a1−b2a1−b3a2−b1a2−b2a2−b3a3−b1a3−b2a3−b3∣∣ ∣∣ then prove that
08:37View Solutionयदि दो रेखाओ के दिक् अनुपात a1,b1,c1 तथा a2,b2,c2 है तो वे परस्पर लंबवत होगी, यदि -
02:54View Solutionयदि →a=a1ˆi+a2ˆj+a3ˆk तथा →b=b1ˆi+b2ˆj+b3ˆk हो तो →a×→b का मान ज्ञात कीजिए।
04:20View Solutionthe value of the determinant
∣∣ ∣ ∣ ∣ ∣∣(a1−b1)2(a1−b2)2(a1−b3)2(a1−b4)2(a2−b1)2(a2−b2)2(a2−b3)2(a2−b4)2(a3−b1)2(a3−b2)2(a3−b3)2(a3−b4)2(a4−b1)2(a4−b2)2(a4−b3)2(a4−b4)2∣∣ ∣ ∣ ∣ ∣∣ is04:57View SolutionSuppose four distinct positive numbers a1,a2,a3,a4 are in G.P. Let b1=a1+,ab=b1+a2,b3=b2+a3andb4=b3+a4.
Statement -1 : The numbers b1,b2,b3,b4 are neither in A.P. nor in G.P.
Statement -2: The numbers b1,b2,b3,b4 are in H.P.01:50View SolutionSuppose a1,a2,a3 are in A.P. and b1,b2,b3 are in H.P. and let Δ=∣∣ ∣∣a1−b1a1−b2a1−b3a2−b1a2−b2a2−b3a3−b1a3−b2a3−b3∣∣ ∣∣ then prove that
12:20View SolutionThe value of the determinant
Δ=∣∣ ∣ ∣ ∣ ∣ ∣∣1−a31b311−a1b11−a31b321−a1b21−a31b331−a1b31−a32b311−a2b11−a32b321−a2b21−a32b331−a2b31−a33b311−a3b11−a33b321−a3b21−a33b331−a3b3∣∣ ∣ ∣ ∣ ∣ ∣∣, is04:27View Solution

