The moment of inertia of semicircular ring about its centre is
MR2
MR22
MR24
None of these
The correct Answer is:A
To find the moment of inertia of a semicircular ring about its center, we can follow these steps:
Step 1: Understand the Geometry of the Semicircular Ring
A semicircular ring is a half-circle with a uniform mass distribution along its length. The center of the semicircle is the point about which we want to calculate the moment of inertia.
Step 2: Define the Moment of Inertia
The moment of inertia (I) about an axis is defined as the sum of the products of the mass elements (dm) and the square of their distances (r) from the axis of rotation:
I=∫r2dm
Step 3: Set Up the Coordinate System
We can set up a polar coordinate system where the semicircular ring lies in the xy-plane. The radius of the semicircular ring is R. The angle θ will vary from 0 to π.
Step 4: Express the Mass Element
The mass element dm can be expressed in terms of the linear mass density λ (mass per unit length) and the arc length element dL:
dm=λdL
For a semicircular ring, the linear mass density is given by:
λ=ML
where L is the length of the semicircular ring, which is 12×2πR=πR. Thus,
λ=MπR
Step 5: Calculate the Arc Length Element
The arc length element in polar coordinates is:
dL=Rdθ
Thus,
dm=MπRRdθ=Mπdθ
Step 6: Calculate the Moment of Inertia
Now, we can substitute dm into the moment of inertia formula:
I=∫π0R2dm=∫π0R2(Mπ)dθ
I=MR2π∫π0dθ
I=MR2π(θ)π0
I=MR2π⋅π=MR2
Final Answer
Thus, the moment of inertia of a semicircular ring about its center is:
I=12MR2
A semicircular ring is a half-circle with a uniform mass distribution along its length. The center of the semicircle is the point about which we want to calculate the moment of inertia.
The moment of inertia (I) about an axis is defined as the sum of the products of the mass elements (dm) and the square of their distances (r) from the axis of rotation:
I=∫r2dm
We can set up a polar coordinate system where the semicircular ring lies in the xy-plane. The radius of the semicircular ring is R. The angle θ will vary from 0 to π.
The mass element dm can be expressed in terms of the linear mass density λ (mass per unit length) and the arc length element dL:
dm=λdL
For a semicircular ring, the linear mass density is given by:
λ=ML
where L is the length of the semicircular ring, which is 12×2πR=πR. Thus,
λ=MπR
The arc length element in polar coordinates is:
dL=Rdθ
Thus,
dm=MπRRdθ=Mπdθ
Now, we can substitute dm into the moment of inertia formula:
I=∫π0R2dm=∫π0R2(Mπ)dθ
I=MR2π∫π0dθ
I=MR2π(θ)π0
I=MR2π⋅π=MR2
Thus, the moment of inertia of a semicircular ring about its center is:
I=12MR2
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on angular momentum)
16 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on kinetic energy, work and power)
30 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on torque, couple)
11 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
Knowledge Check
A semicircular disc of mass M and radius R is free to rotate about its diameter. The moment of inertia of semicircular disc about a line perpendicular to its plane through centre is
A34MR2BMR22CMR23DMR24The moment of inertia of a circular ring about one of its diameters is I . What will be its moment of inertia about a tangent parallel to the diameter?
A4 IB2 IC32ID3IThe moment of inertia of a semicircular ring of mass M and radius R about an axis which is passing through its centre and at an angle θ with the line joining its ends as shown in figure is
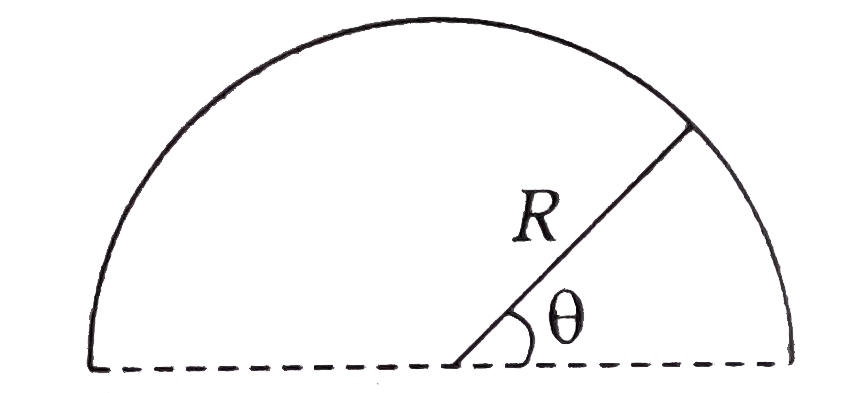 AMR24ifθ=0∘BMR22ifθ=0∘CMR22ifθ= any angleDMR22ifθ=90∘
AMR24ifθ=0∘BMR22ifθ=0∘CMR22ifθ= any angleDMR22ifθ=90∘
The moment of inertia of a circular ring about an axis passing through its diameter is I . This ring is cut then unfolded into a uniform straight rod. The moment of inertia of the rod about an axis perpendicular to its length passing through one of its ends is
View SolutionThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
View SolutionMoment of inertia of a circular ring about an axis through its centre and perpendicular to its plane is
View SolutionI is moment of inertia of a thin circular ring about an axis perpendicular to the plane of ring and passing through its centre. The same ring is folded into 2 turns coil. The moment of inertia of circular coil about an axis perpendicular to the plane of coil and passing through its centre is
View SolutionThe moment of inertia of a ring about one of its diameter is 2kgm2 . What will be its moment of inertia about a tangent parallel to the diameter?
View Solution
