A ring of radius 4a is rigidly fixed in vertical position on a table. A small disc of mass m and radius a is released as shown in the fig. When the disc rolls down, without slipping, to the lowest point of the ring, then its speed will be
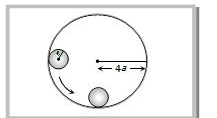
√ga
√2ga
√3ga
√4ga
The correct Answer is:D
Step by step video, text & image solution for A ring of radius 4a is rigidly fixed in vertical position on a table. A small disc of mass m and radius a is released as shown in the fig. When the disc rolls down, without slipping, to the lowest point of the ring, then its speed will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)
10 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on kinetic energy, work and power)
30 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
A ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.



View SolutionA uniform disc of mass M and radius R is rotating freely about its central vertical axis with angular speed w0. Another disc of mass m and radius r is free to rotate about a horizontal rod AB. Length of the rod AB isL(<R) and its end A is rigidly attached to the vertical axis of the first disc. The disc of mass m, initially at rest, is placed gently on the disc of mass M as shown in figure. Find the time after which the slipping between the two discs will cease. Assume that normal reaction between the two discs is equal to mg. Coefficient of friction between the two discs is μ.

View Solution
Knowledge Check
A disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is
 A−52mR2ωˆkB73mR2ωˆkC−92mR2ωˆkD52mR2ωˆk
A−52mR2ωˆkB73mR2ωˆkC−92mR2ωˆkD52mR2ωˆkAs shown in the figure, a disc of mass m is rolling without slipping with angular velocity ω. When it crosses point B disc will be in
 Atranslational motion onlyBpure rolling motionCrotational motion onlyDnone of these
Atranslational motion onlyBpure rolling motionCrotational motion onlyDnone of theseA force F acts tangentially at the highest point of a disc of mass m kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:
 A2F3mB10F7mCzeroD4F3m
A2F3mB10F7mCzeroD4F3m
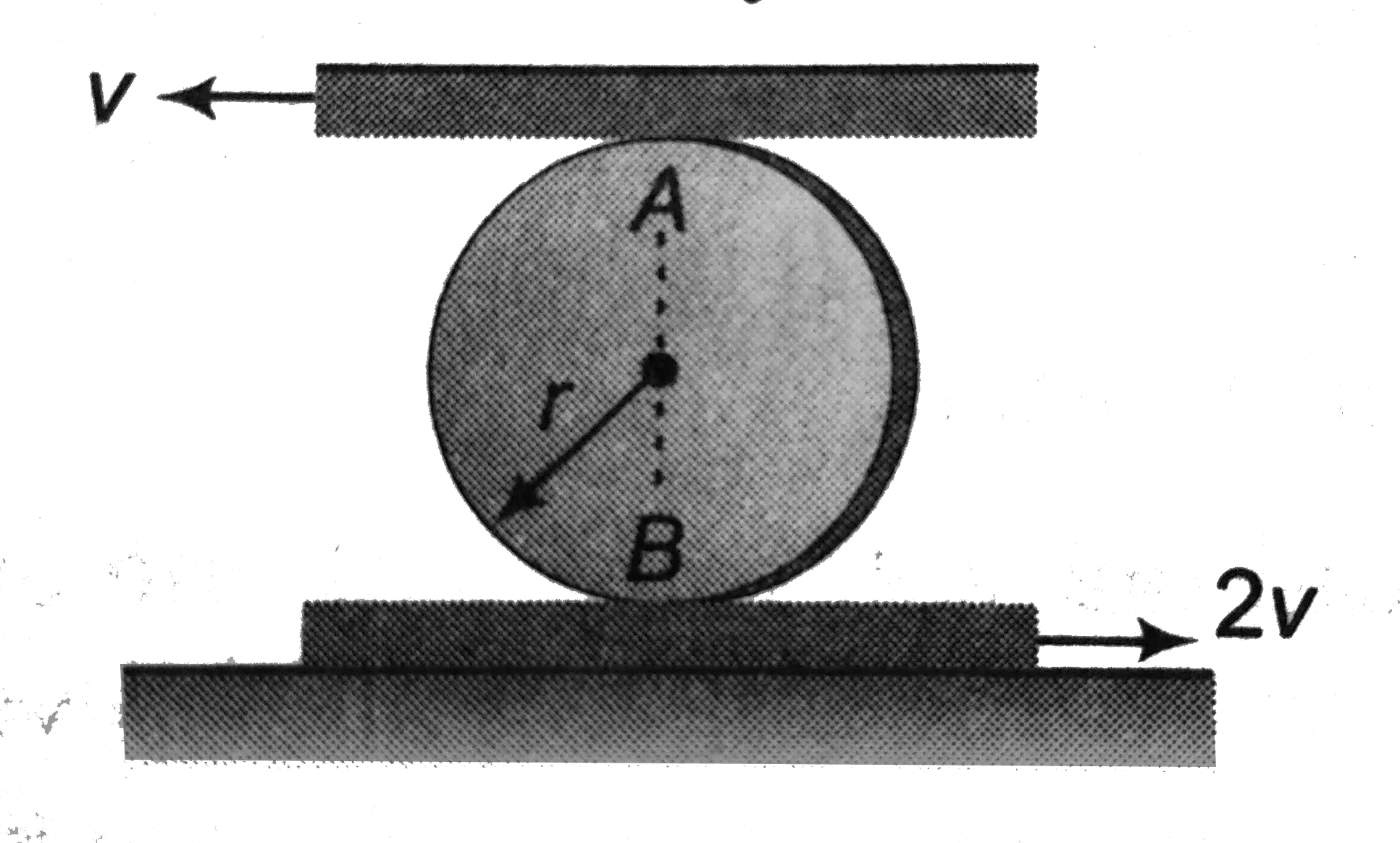
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA particle of mass 'm' is rigidly attached at 'A' to a ring of mass 3m and radius 'r' . The system is released from rest and rolls without sliding. The angular release is acceleration of ring just after release after

View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View SolutionA ring of mass M and radius R is at rest at the top of an incline as shown. The ring rolls down the plane without slipping. When the ring reaches bottom, its angular momentum about its centre of mass is:
View Solution
