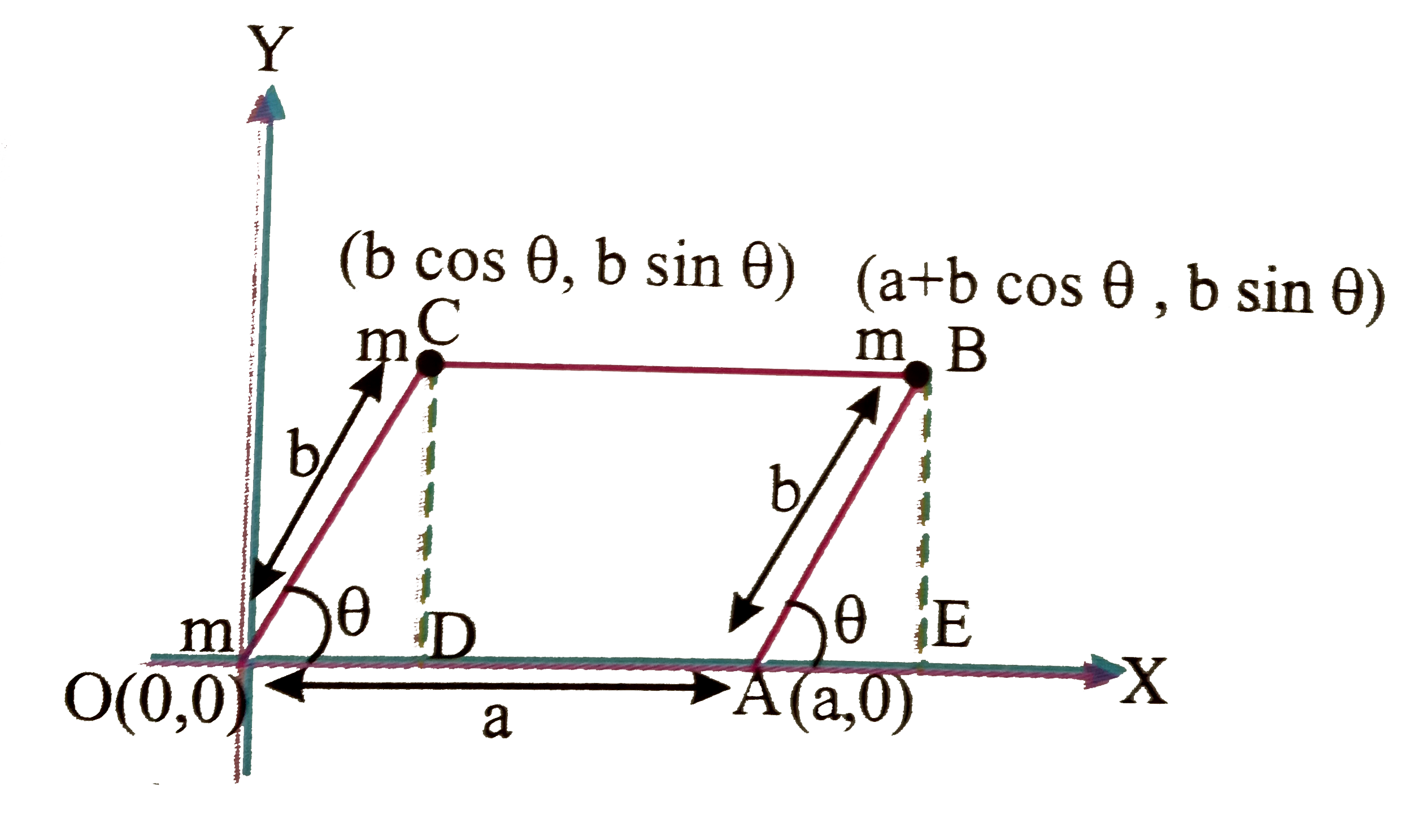Find position of centre of mass of four particle system, which are at the vertices of a parallelogram, as shown in figure.
Text Solution
Consider four particles of each of mass .m. placed at the vertices of a parallelogram. Let a and b be the length and breadth of parallelogram as shown in figure and θ be angle between ¯a and ¯b
In the parallelogram OABC, identical masses .m. each are placed at its vertices.
From triangle OCD
DC=bsinθ, OD=bcosθ
∴ the co-ordinates of vertex C[x4,y4]=[bcosθ,bsinθ]
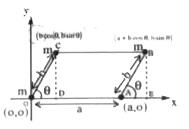
from triangle ABE
BE=bsinθAE=bcosθ
and OE=OA+AE=a+bcosθ
∴ The co-ordinates of vertex B[x3y3]=[a+bcosθ,bsinθ]
Also co-ordinates of vertices O(x1,y1)=[0,0] and A(x2,y2)=[a,0]
we know , x co-ordinate of centre of mass
xcm=m1x1+m2x2+m3x3+m4x4m1+m2+m3+m4
xcm=m(0)+m(a)+m(a+bcosθ)+m(bcosθ)4m
Xcm=2a+2bcosθ4, xcm=[a+bcosθ]2
we know y-co-ordinate of centre of mass is
ycm=m1y1+m2y2+m3y3+m4y4m1+m2+m3+m4
ycm=m(0)+m(0)+m(bsinθ)+m(bsinθ)4m
ycm=(2bsinθ)/(4)=bsinθ2
∴ Position co-ordinate [xcm,ycm] of centre of mass is [a+bcosθ2,bsinθ2].
Case-I : If masses are arranged at vertices of a rectangle then θ=90∘
∴[xcm,ycm]=[a+bcos90∘2,bsin90∘2]=[a2,b2]
Case-II : If masses are arranged at vertices of a square, then θ=90∘ and lengths of sides are equal (a=b).∴[xcm,ycm]=[a2,a2]
|
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Exercise-I
143 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Exercise-II
109 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE (Rotational Dynamics )
17 Videos
- SURFACE TENSIONBOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )
8 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
Similar Questions
Knowledge Check
The position of centre of mass of a system of particles does not depend upon
Amasses of particlesBforces on particlesCposition of the particlesDrelative distance between the particles
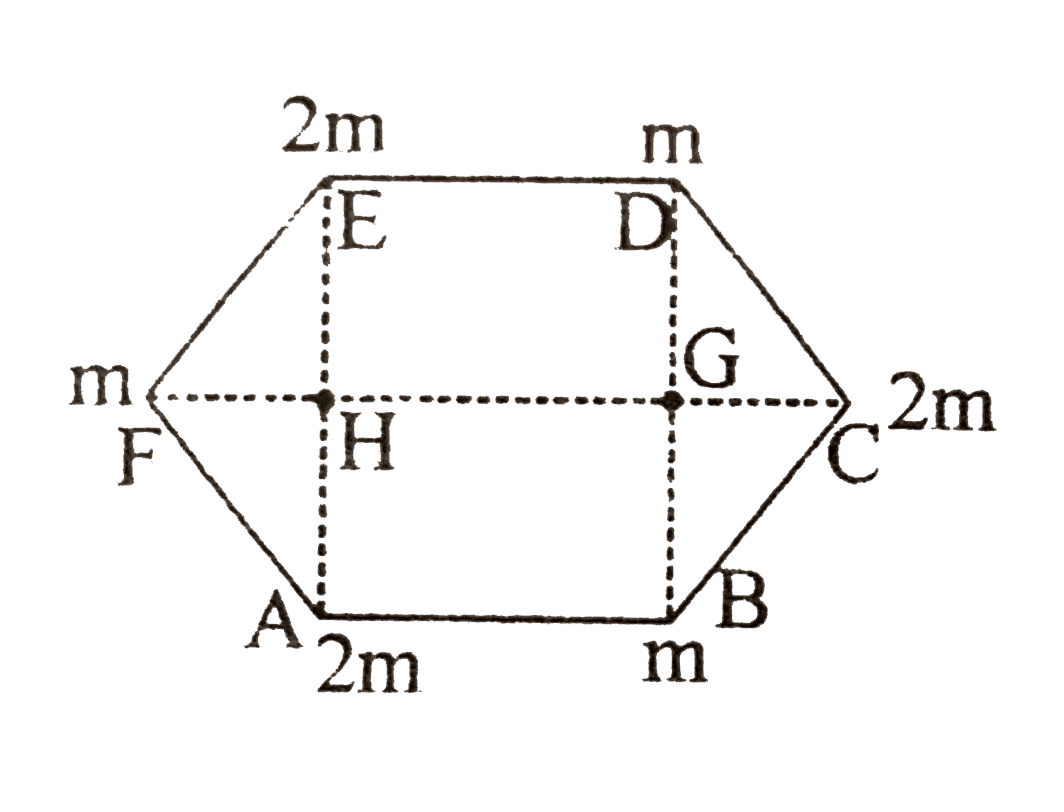
Find the position of centre of mass for a system of particles places at the vertices of a regular hexagon as shown in figure
View SolutionFind the position of centre of mass of the section shown in figure

View SolutionFind the position of centre of mass of the section shown in figure

View SolutionFind out the position of centre of mass of the figure shown below.
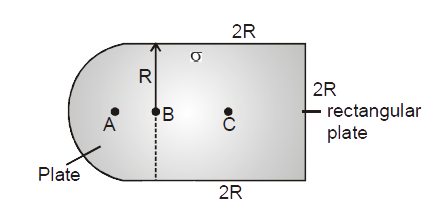
View SolutionFind centre of mass of a system of three particle kept at the corner equilateral triangle as shown in figure
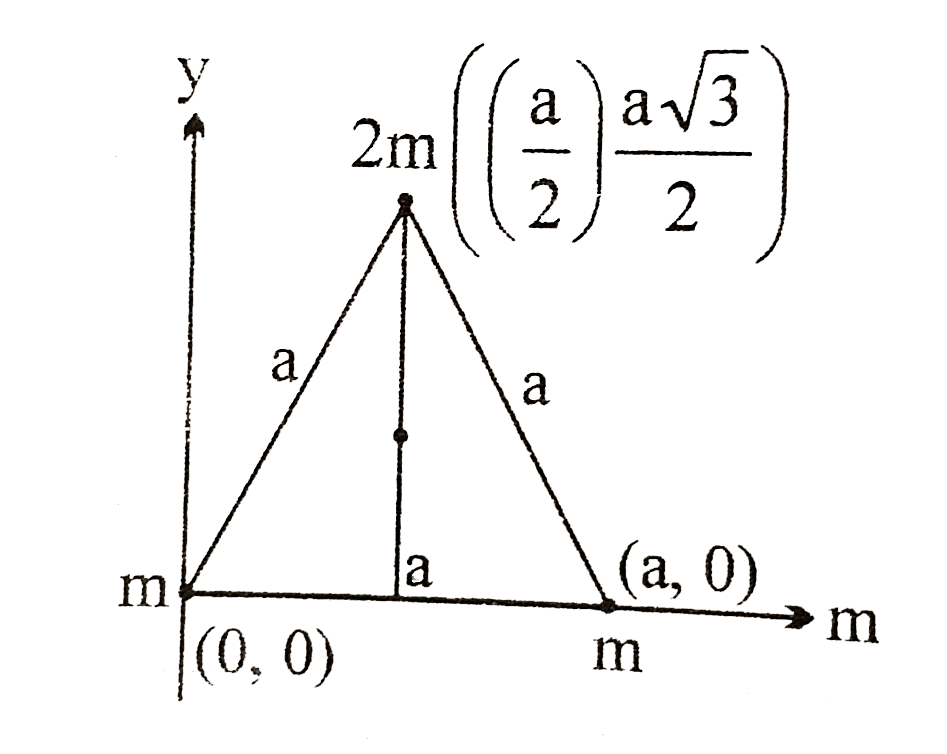
View SolutionFind the position of centre of mass of the uniform lamina shown in figure.
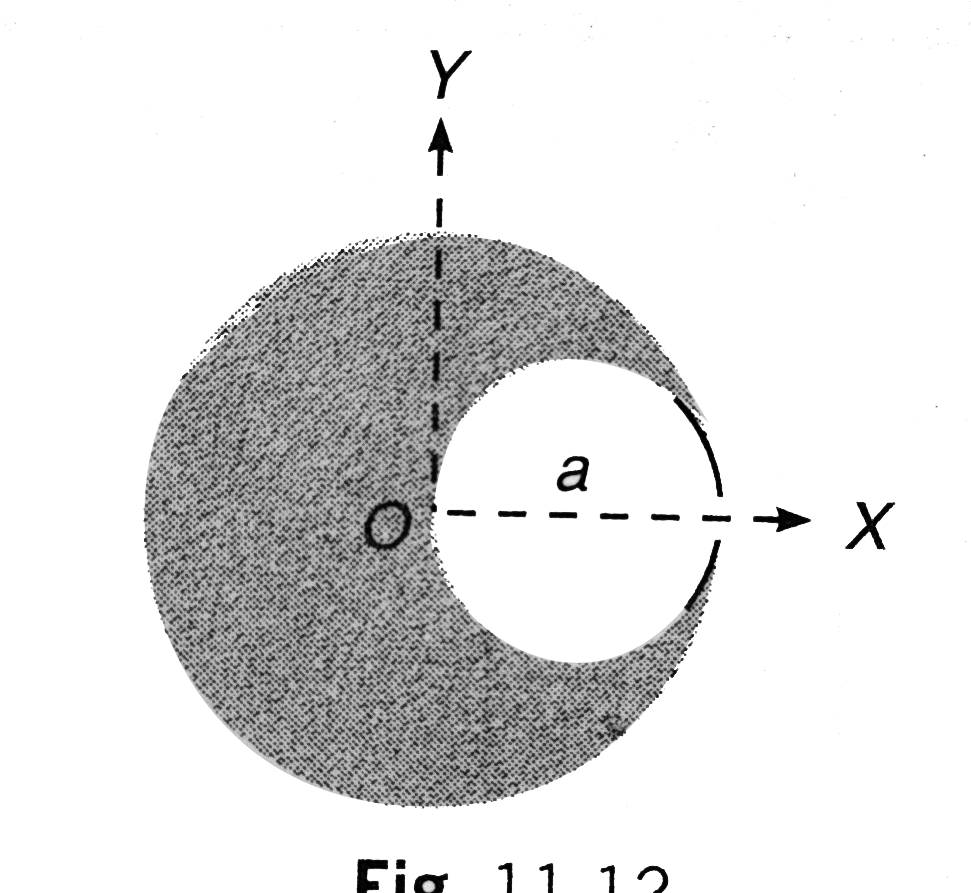
View SolutionFind the position of centre of mass of the uniform lamina shown in figure.

View Solution