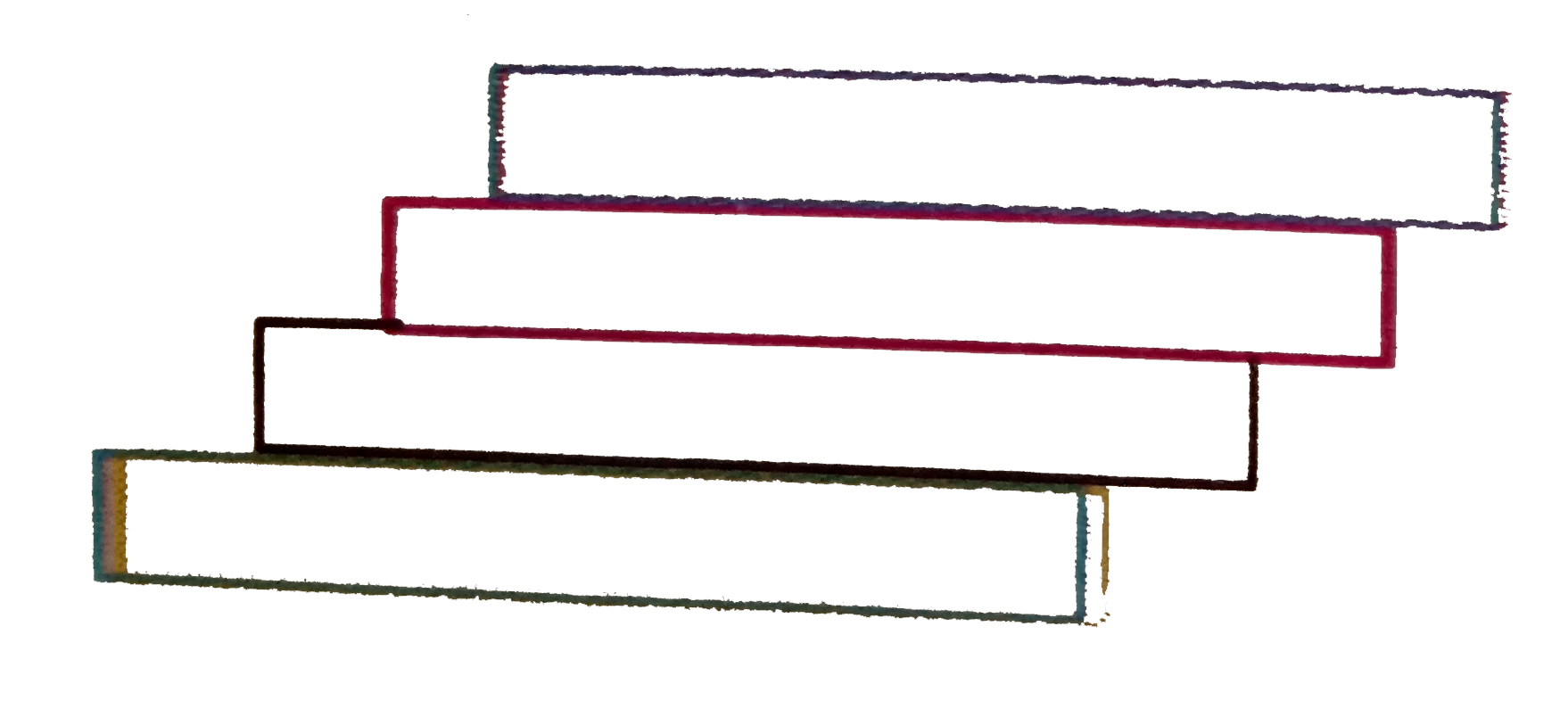
Identical blocks each of mass M and length L are placed one above the other such that each extends out by maximum length as shown in figure. Find the maximum extension of the nth block from the top. So that the blocks will not fall.

For a two block system, the center of mass (C1) of upper block should be at the edge of lower block . i.e. at l/2 distance. But if center of mass of upper block is not resting on the lower block then , the upper block falls down because of unbalanced torque created by gravitational force
 x1=l2
x1=l2
If a third block (EF) is arranged below the two blocks then

The center of mass (C2) of (AB) and (CD) block system must lie on the edge E of third block. To find x2 consider C as origin. Then
x2=M(0)+M(l2)2M=l4
∴x2=l4 So, center of mass of upper two blocks is at l4 distance from edge of lower block. Also, if another block (GH) is placed below the three blocks in equilibrium, then

The center of mass (C3) of the upper three blocks must lie on the edge of the lower fourth block i.e. at G. To find x3 consider E as origin
x3=2M(0)+M(l2)3M=l6 ∴x3=l6
Simillarly x4=l8, x5=l10, .......
For nth block xn=l2n
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Exercise-I
143 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Exercise-II
109 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE (Rotational Dynamics )
17 Videos
- SURFACE TENSIONBOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )
8 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
Similar Questions
Identical blocks each of mass M and length L are placed one above the other such that each extends out by a maximum length as shown in figure. Find the maximum extension of the nth block from the top, so that the blocks will not fall.
View SolutionTwo blocks A and B each of equal masses m are released from the top of a smooth fixed wedge as shown in the figure. Find the magnitude of the acceleration of the centre of mass of the two blocks.

View Solution
Knowledge Check
Four identical rods of mass M and length L are placed on one another on the table so as to produce the maximum overhang as shown in figure. The maximum total overhang will be :
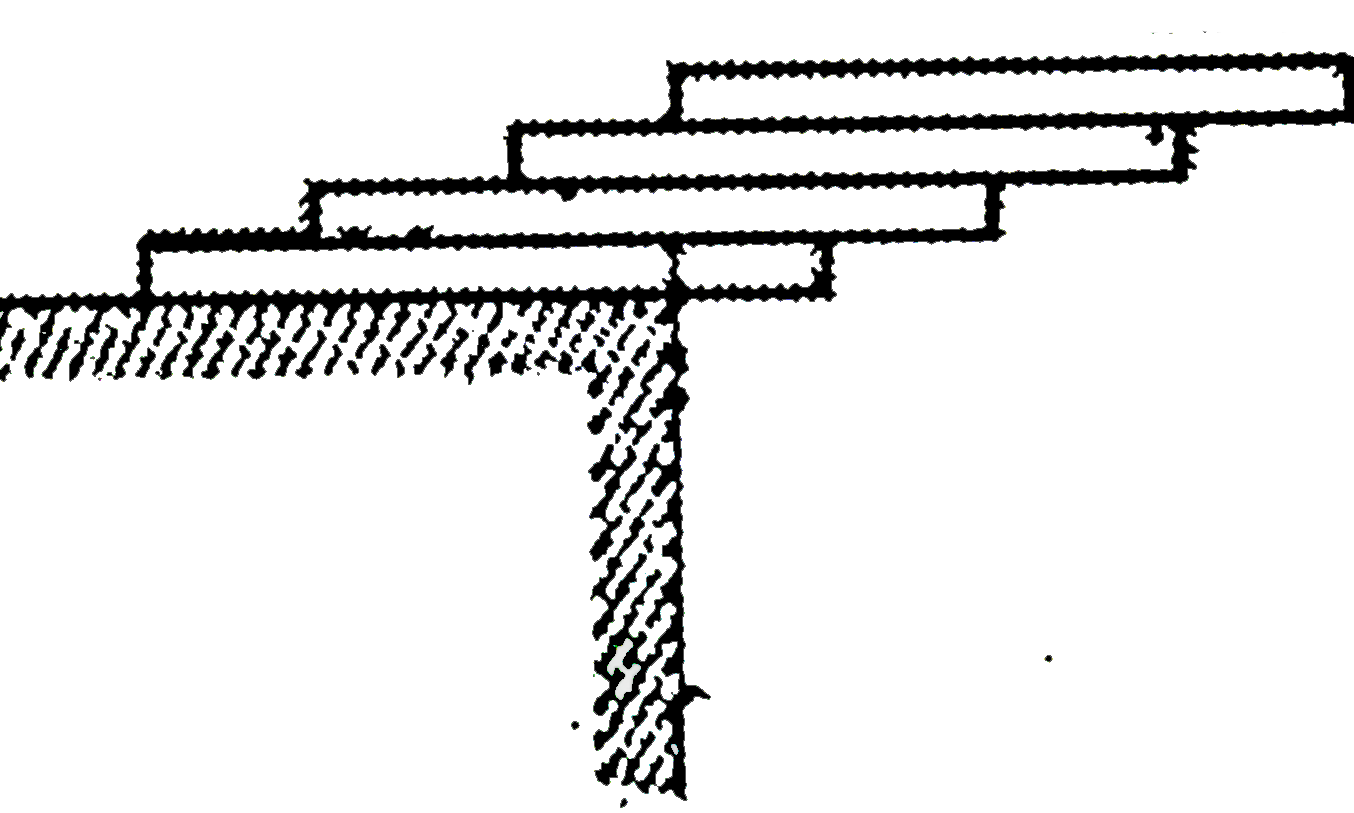 A3L4B24L25C25L24D4L3
A3L4B24L25C25L24D4L3The block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is
 AkL22MB√MkL(c)SCML2kDzero
AkL22MB√MkL(c)SCML2kDzeroA block of mass 1 kg is placed on a wedge shown in figure. Find out minimum coefficient of friction between wedge and block to stop the block on it.
 A0.6B0.9C1D0.2
A0.6B0.9C1D0.2
Two blocks A and B each of equal masses m are rleased from the top of a smooth fixed wedge as shown in the figure. Find the magnitude of the accelertion of the centre of mass of the two blocks.

View SolutionThree identical blocks each of mass M are along a frictionless table and a force F is acting as shown. Which of the following statements is false ?
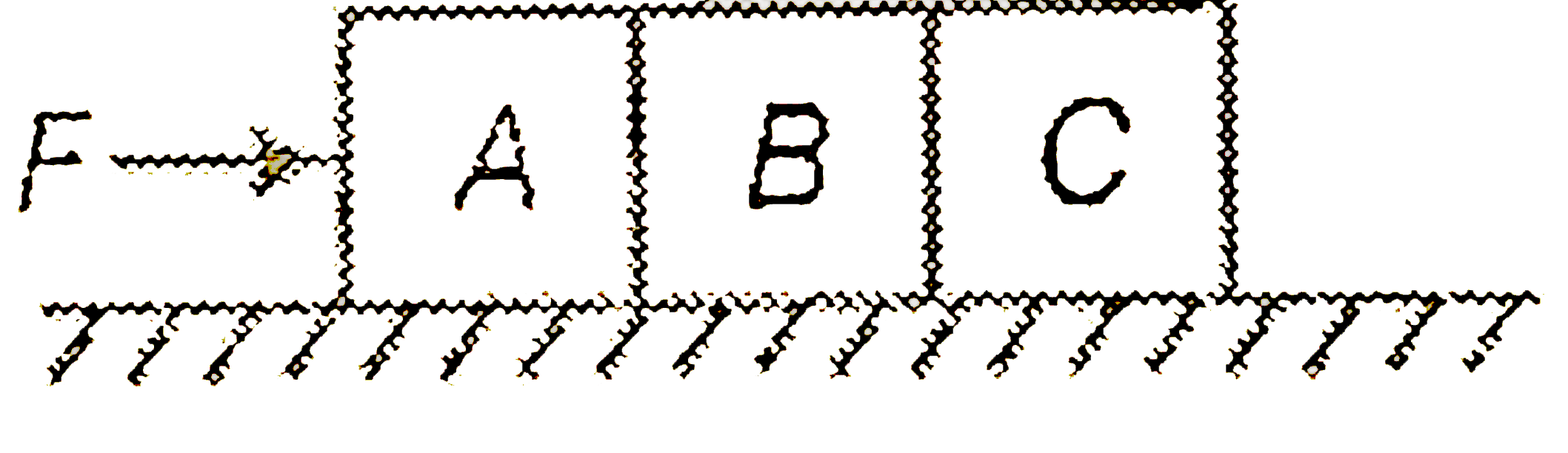
View SolutionThe block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is

View SolutionThree identical blocks, each having a mass m are pushed by a force F on the Frictionless table as shown in figure.
What is the net force on the block A?

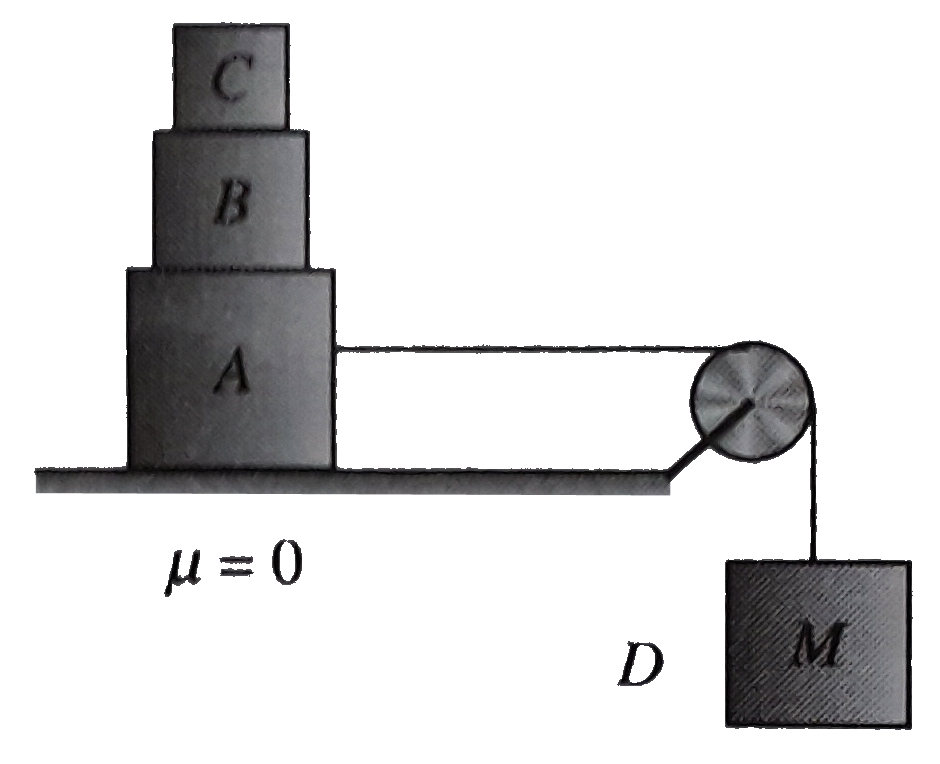
View SolutionThere block A B ,and C of equal mass m are placed one over the other on a frictionless surface (table) as shown in figure The coefficient of friction between any blocks A ,B and C is μ The maximum value of mass of block D so that the blocks A,B and C move without slipping over each other is
View Solution
