A massless string is wrapped around a disc that has a radius of 10cm and mass of 1.500kg. The free end of the string is attached to a hanging block of mass 1.000kg, the other end is fixed to a point on the rim of the disk . Neglecting friction, find the linear acceleration of the hanging block if the block is released from rest. (g=10ms−2)

Let .M. and .m. be the masses of the disc and block respectively. R is the radius of the disc. Linear acceleration of the block is .a.. The forces on the block are
(i) gravitational force, mg and
(ii) the tension T in the string
Since the block moves down we have
mg−T=ma.............(1)
This acceleration a is due to the torque acting on the disc
Torque on the disc τ=T×R Iα=TR
MR22aR=TR or T=Ma2
Substituting T in equation ............(1)
ma=mg−Ma2 on solving a=mg(m+M2)
a=1(10)(1+1.52)=101.75=5.714ms−2
T=1.5×5.7142=4.28N
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Exercise-I
143 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Exercise-II
109 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE (Rotational Dynamics )
17 Videos
- SURFACE TENSIONBOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )
8 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
Similar Questions
A mass less string is wrapped around a uniform disc of mass m and radius r. The string passes over a mass less pulley and is tied to a block of mass M at its other end (see figure). The system is released from rest. Assume that the string does not slip with respect to the disc.
(a) Find the acceleration of the block for the case M=m
(b) Find Mm for which the block can accelerate upwards.
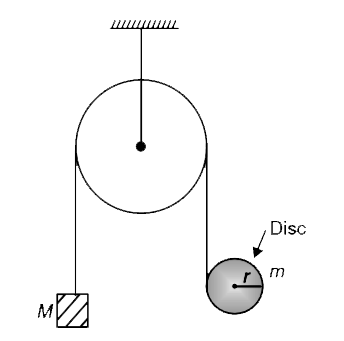
View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View Solution
Knowledge Check
A string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
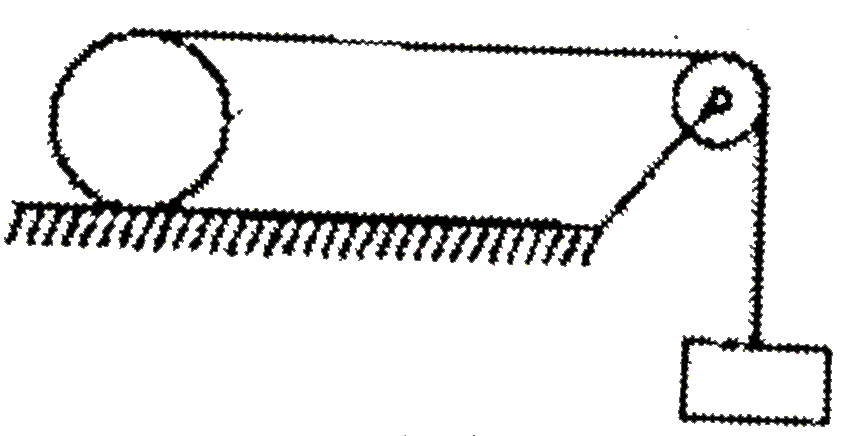
Velocity of hanging block at this moment is: is:A√2πRgB√8πRgC√πRg2D√45πRgA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
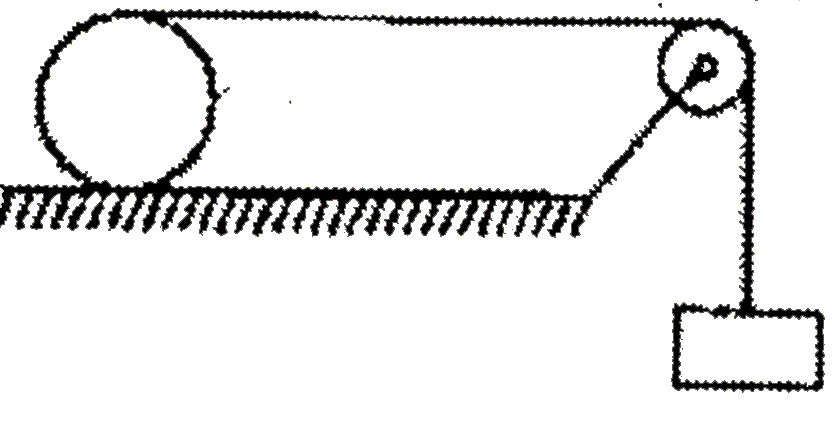
Acceleration of hanging mass is:AgBg2Cg4D3g4A string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
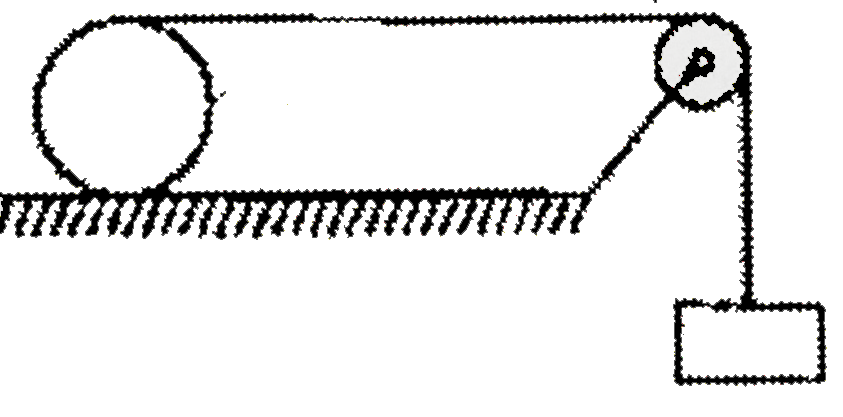
Acceleration of cylinder is:AgBg2Cg4D3g4
A block of mass 2 kg is kept at rest on a smooth inclied plane as shown in (a) with the help of a string Find the tension in the string and reaction on the block if the string is cut, find the acceleration of the block neglecting friction.
View SolutionTwo blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of centre of mass of the two blocks when they are released from rest. Neglect friction.

View SolutionTwo blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of centre of mass of the two blocks when they are released from rest. Neglect friction.

View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
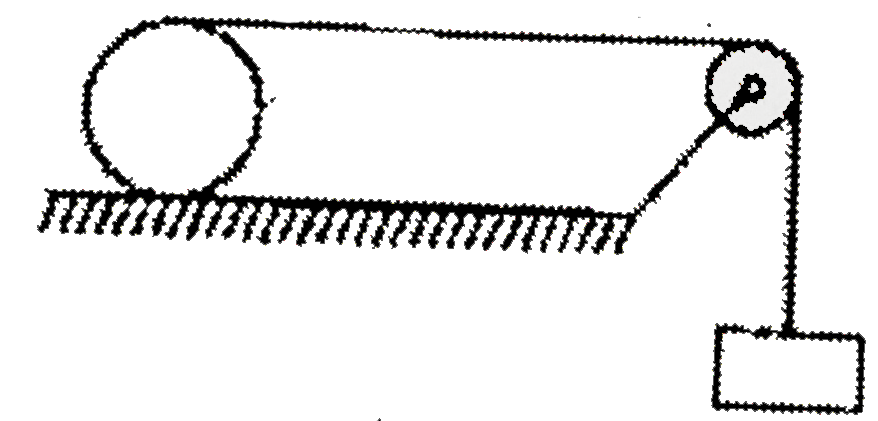
Velocity of point of contact 'of cylinder at this moment is:
View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View Solution
