A uniform rod AB of mass 'm' length 2a is allowed to fall under gravity with AB in horizontal. When the speed of the rod is 'v', suddenly the end 'A' is fixed. Find the angular velocity with which it begins to rotate .
L1=L2
mva=Iω
mva=m(2a)23ω⇒ω=3v4a

Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Exercise-I
143 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Exercise-II
109 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE (Rotational Dynamics )
17 Videos
- SURFACE TENSIONBOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )
8 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
Similar Questions
A uniform rod AB of mass m and length 2a is falling freely without rotation under gravity with AB horizontal. Suddenly the end A is fixed when the speed of the rod is v. The angular speed which the rod begains to rotate is
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?
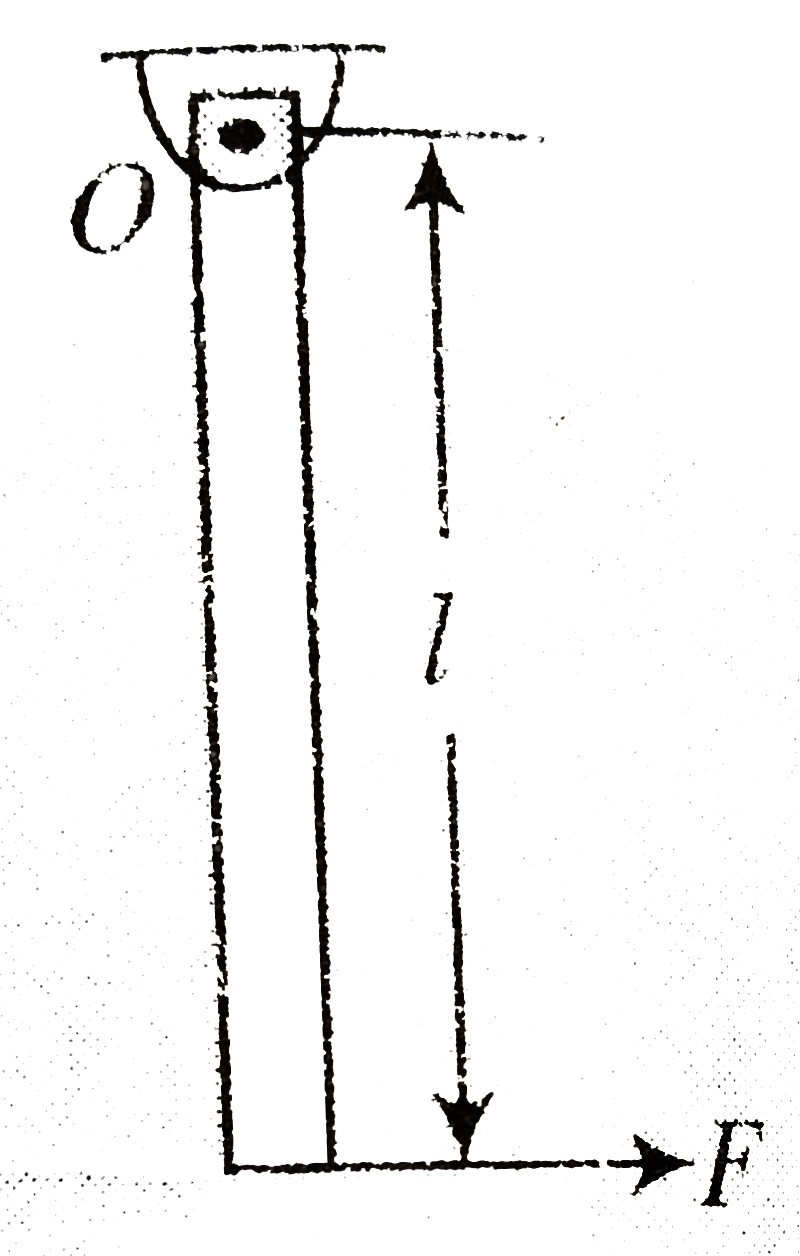
View Solution
Knowledge Check
A uniform rod AB of mass m and length 2a is falling freely without rotationb under gravity with AB horizontal. Suddenly the end A is fixed when the speed of the rod is v. The angular speed which the rod begains to rotate is
Av2aB4v3aCv3aD3v4aA uniform rod AB of length l rotating with an angular velocity ω while its centre moves with a linear velocity v=ωl6 If the end A of the rod is suddenly fixed, the angular velocity of
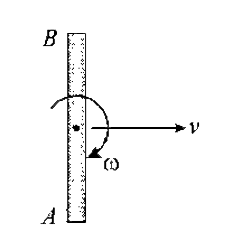 A34ωBω3Cω2D23ω
A34ωBω3Cω2D23ω
A uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?
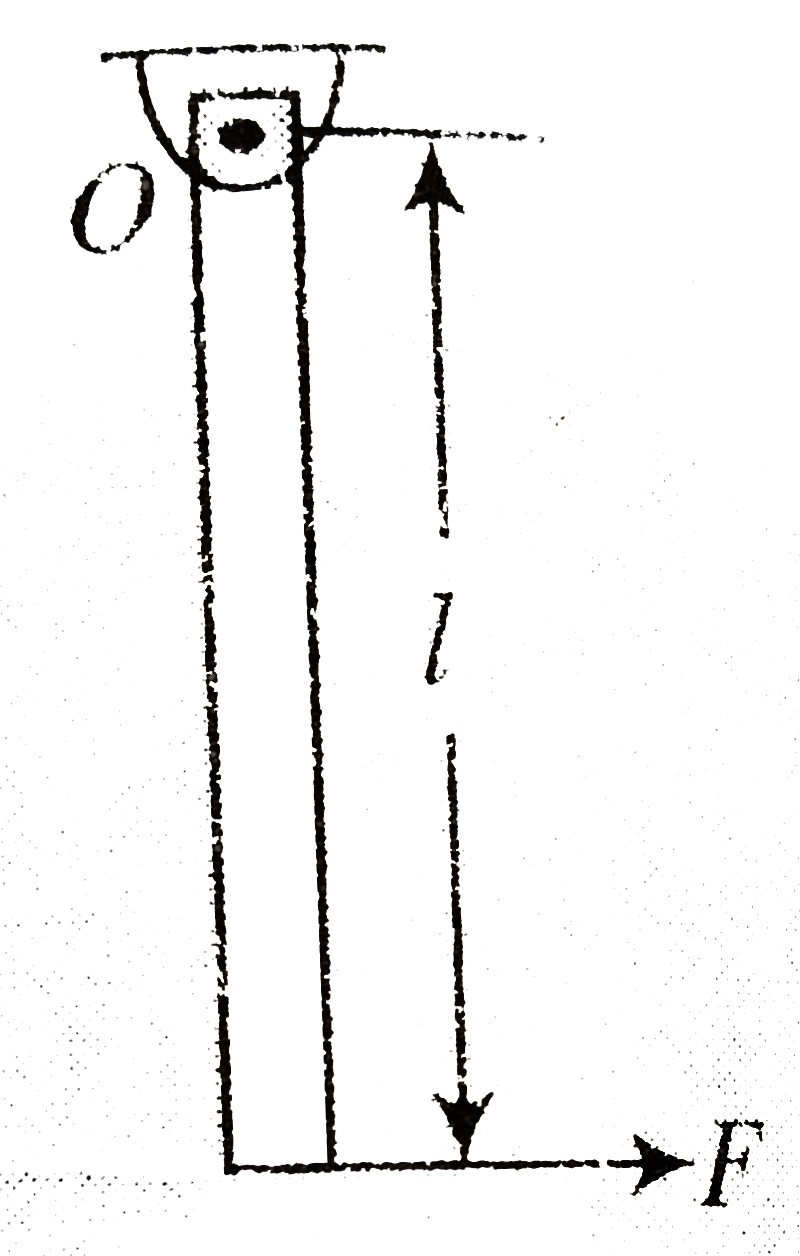
View SolutionA uniform rod of mass m=2kg and length l is kept on a smooth horizontal plane. If the ends A and B of the rod move with speeds v and 2v respectively perpendicular to the rod, find the:
a. angular velocity of CM of the rod.
b. Kinetic energy of the rod (in Joule).

View SolutionA uniform rod of mass m=2kg and length l is kept on a smooth horizontal plane. If the ends A and B of the rod move with speeds v and 2v respectively perpendicular to the rod, find the:
a. angulr velocity of CM of the rod.
b. Kinetic energy of the rod (in Joule).

View SolutionA uniform rod of length l is held vertically on a horizontal floor fixing its lower end, the rod is allowed to fall onto the ground. Find (i) its angular velocity at that instant of reaching the ground (ii) The linear velocity with which the tip of rod hits the floor.
View SolutionA conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity ω(the upper end of the rod is hinged). Find the angle θ between the rod and the vertical.
View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.

View Solution
