A uniform sphere has radius R . A sphere of diameter R is cut from its edge as shown. Then the distance of centre of mass of remaining portion from the centre of mass of the original sphere is
Solution in Telugu
The correct Answer is:B
Step by step video & image solution for A uniform sphere has radius R . A sphere of diameter R is cut from its edge as shown. Then the distance of centre of mass of remaining portion from the centre of mass of the original sphere is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Exercise-II109videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )8videos
SURFACE TENSION
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions2videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Centre of mass of two particle with masses 2 kg and 1 kg locsted at (1, 0, 1) and (2, 2, 0) has the co - ordinates of
08:56View SolutionIf the work done in blowing a soap bubble of volume 'V' is W, then the work done in blowing a soap bubble of volume '2V' is
03:20View SolutionA constant pressure gas thermometer has a volume of 200cc, 273.2cc and 525 .1cc at 0°C, 100°C and boiling point of sulphur respectively. The resistance possessed by a platinum wire at the same temperatures as above are 2.000Ω,2.778Ωand5.280Ω respectively. Estimate the boiling point of sulphur on the basis of the two sets of observations.
03:57View SolutionA uniform sphere has a mass M and radius R. Find the pressure p inside the sphere, caused by gravitational compression, as a function of the distance r from its centre. Evaluate p at the centre of the Earth, assuming it to be a uniform sphere.
05:14View SolutionA uniform sphere has radius R. A sphere of diameter R is cut from its edge as shown. Then the distance of centre of mass of remaining portion from the centre of mass of the original sphere is
02:41View SolutionThere is a concentric hole of radius R in a solid sphere of radius 2R. Mass of the remaining portional is M. What is the gravitational potential at centre?
05:48View SolutionDistance between centres of two spheres A andB, each of radius R is r as shown in figure -1.450 . SphereB has a spherical cavity of radius R//2 such that distance of centre of cavity is (r-R/2) from the centre of sphere A and R//2 from the centre of sphere B. Di-electric constant of material of each sphere is K = I and material of each sphere has a uniform charge density· p per unit volume. Calculate interaction energy of the two spheres :
06:15View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
08:12View SolutionA semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is
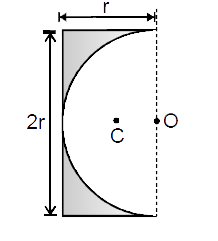
05:20View SolutionA particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R . A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is (lambdaGMm)/(28R) . Find the value of lambda
05:43View SolutionThe radius of a uniform sphere is R and its mass is M. The values of the gravitational intensity at distance r_1 and r_2 from the centre of the sphere are F_1 and F_2 respectively. Then,
01:57View SolutionA sphere of diameter r is cut from a solid circle of radius r such that if the center of mass of the remaining part is at maximum distance from the center of the original circle, then the distance is -
05:17View SolutionA uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the centre of the sphere while the other is at the boundary. Locate centre of mass of the remaining sphere..
04:56View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
08:11View Solution_E01_035_Q01.png)
There is a concentric hole of radius R in a solid sphere of radius 2R. Mass of the remaining portional is M. What is the gravitational potential at centre?04:34View Solution